算法-蓝桥杯第十五届抱佛脚（六）回溯与剪枝

蓝桥杯第十五届抱佛脚（六）回溯与剪枝

基本概念

想象一下，你在玩一个迷宫游戏。你的目标是从迷宫的入口走到出口。这个迷宫有很多的岔路口，每个岔路口都可以向几个不同的方向走。但是，并不是所有的路径都会带你到出口，有些可能会带你进入死胡同。那么，你如何找到一条正确的路径呢？

这里就可以用到回溯算法（Backtracking）。你可以这样理解它：

尝试：从迷宫的入口开始，随意选择一个方向走。
探索：继续前进，每到一个新的岔路口就再次随意选择一个方向。
回溯：如果你走到了死胡同（也就是这条路不可能让你到达出口），你就回到上一个岔路口，尝试选择一个不同的方向。

这样，通过在岔路口做决策，如果发现当前路径不通，就退回到上一个岔路口，这就是回溯算法的基本思想。在编程中，我们通常用递归函数来模拟这一过程。

但是，如果迷宫非常大，这样盲目地尝试每一个方向会非常耗时，因为可能性太多了。这时候就需要剪枝（Pruning）了。

剪枝可以理解为在迷宫游戏中用一些智能的策略来避免无意义的探索：

规则剪枝：比如，如果你已经知道迷宫的某些区域肯定没有出口，你就可以直接避开那些区域，不去探索。
预测剪枝：或者，如果你发现前方的路径看起来和已知的死胡同非常相似，那么你可以根据经验提前回头，而不是继续前进直到真正走进死胡同。这就好比在迷宫中，如果看到前面的路越来越窄，你可以推断这条路可能会走不通。

回溯和剪枝一起使用时，就像你带着一个地图和指南针进入迷宫。地图上有标记，告诉你哪些区域是没有出口的（规则剪枝），指南针可以告诉你当前的方向是否可能正确（预测剪枝）。你不断地尝试，每当遇到死路，就回到上一个岔路口，再次尝试其他路线。同时，你也会记住那些无用的路径，以避免重复探索它们。

在实际的编程问题中，比如解决数独或者八皇后问题时，我们会用回溯算法来尝试每一种可能的解决方案。当我们发现当前的方案不会导致一个有效的完成（就像在迷宫中走进了死胡同），我们会退一步（递归函数的回退）并尝试其他的选项。剪枝则是在这个过程中的优化，它能帮助我们避免探索那些显然无效或者不太可能的路径。

回溯算法

回溯算法的工作原理

回溯算法是一种解决问题的算法，它尝试解决问题的一个分支，如果发现当前分支不能得到有效的完整解决方案，就会消除（回溯）所做的一系列选择，并尝试另一个可能的分支。回溯算法通常用于解决组合问题，如排列、组合、选择和分割问题，它通过逐步构建解的候选项并在每个步骤中继续或放弃继续探索的决策，实现问题的穷举搜索。

算法的步骤和结构框架

确定解空间：首先需要明确问题的解空间，即解决问题的全部候选解的集合，常常通过状态空间树表示。
确定搜索策略：回溯算法通常采用深度优先搜索策略（DFS）来遍历状态空间树。
实施搜索过程：从树的根节点（问题的初始状态）出发，深入探索每一个分支，直到找到可能的解或到达无法继续的节点。
应用剪枝函数：在搜索过程中，适时使用剪枝函数避免无效的搜索。
回溯条件：当达到无法继续或找到一个解后，回溯到上一个节点，放弃上一个决策，尝试其他选项。
输出解或继续搜索：当找到一个可行解时，可以输出此解或记录下来；如果解不可行或需要寻找所有解，继续遍历其他分支。

回溯算法框架：

void backtrack(List<Integer> path, int start, int[] nums) {
    // 成功找到一个解并结束当前路径的递归
    if (isSolution(path)) {
        results.add(new ArrayList<>(path));
        return;
    }
    
    // 从start开始遍历每个可能的选项
    for (int i = start; i < nums.length; i++) {
        // 检查当前的选择是否符合约束
        if (isValidChoice(nums[i], path)) {
            // 做出选择，将当前选项加入到路径中
            path.add(nums[i]);
            
            // 递归进入下一层决策树
            backtrack(path, i + 1, nums);
            
            // 撤销选择，回溯到上一步
            path.remove(path.size() - 1);
        }
    }
}

boolean isSolution(List<Integer> path) {
    // 实现检查路径是否构成一个解的逻辑
}

boolean isValidChoice(int choice, List<Integer> path) {
    // 实现检查当前选择是否有效的逻辑
}

// 主函数入口
void findSolutions(int[] nums) {
    List<Integer> path = new ArrayList<>();
    backtrack(path, 0, nums); // 从第一个元素开始回溯搜索
}

// 在某处存储所有解
List<List<Integer>> results = new ArrayList<>();

我们定义了一个 backtrack 方法，它尝试对输入数组 nums 中的每个元素进行决策，并构建解的路径 path。该方法首先检查 path 是否构成了一个完整的解，如果是的话，将其添加到 results 列表中。接着，算法递归地对每个可能的选项进行探索，检查每个选项是否有效，然后在选项有效的情况下，选择该选项并进一步递归，最后在递归返回后撤销选择。这个过程中的剪枝可以在 isValidChoice 方法中实现，通过适当的逻辑来避免无效的搜索路径。

在实际编写Java程序时，你需要根据实际问题定义 isSolution 和 isValidChoice 方法的具体逻辑。

递归与回溯的关系

递归是回溯算法实现的一种常用技术，每一次递归调用都对应于状态空间树中的一次深入探索，每一次递归返回都对应于状态空间树中的一次回溯。递归使得状态空间树的深入和回溯过程变得自然，因为它天然地通过函数调用栈来保存状态。

在递归过程中，每一层递归函数代表了解空间树的一层，递归参数代表了当前节点的状态，递归函数内部进行分支选择，根据问题约束条件判断是否继续递归或是回溯。如果当前递归路径不满足问题的约束条件，递归将返回，相当于在状态空间树中回溯到上一层节点，尝试其他可能的分支。这样递归与回溯配合，系统地搜索整个解空间。

剪枝

剪枝的定义和目的

剪枝是指在回溯算法过程中，根据某些规则提前停止对无效路径的探索的技术。目的是提高算法效率，减少不必要的计算，缩短算法运行时间。

剪枝的不同类型：

预测性剪枝：基于对当前探索路径未来发展的预测，如果预测表明这条路径不可能产生有效或最优解，则提前终止。
可行性剪枝：在探索过程中，如果发现当前路径不满足问题的基本约束条件，即判定为不可行，那么就停止进一步探索。
最优性剪枝：特别用于求解最优化问题。如果当前路径的部分解已经不可能优于已找到的最佳解，则舍弃该路径。

剪枝在实际应用中的例子：
在解决八皇后问题时，通过检查当前皇后的位置是否会受到其他皇后的攻击（可行性剪枝），如果会，就不继续在这条路径上探索。

剪枝对算法效率的影响分析：
剪枝大幅减少了搜索空间和搜索时间。在最优情况下，剪枝可以将指数级的复杂度降低至多项式级别，但具体效果依赖于问题本身和剪枝策略的有效性。

算法设计和实现

回溯算法的通用设计模式：

递归框架：定义一个递归函数，表示在某个状态下的探索。
路径记录：使用数据结构（如列表或数组）记录当前路径或选择。
回溯点：在每次递归调用前后，分别执行选择和撤销选择的操作。

剪枝技术的具体实现方法：

在递归前进行条件检查，如是否符合约束，是否已经不优于当前最优解等。
使用全局变量或传递参数来保存当前最优解，以用于最优性剪枝。

示例代码：

void backtrack(Path path, Params params) {
    if (path not valid) return; // 可行性剪枝
    if (path is complete) {
        update solution; // 找到一个解
        return;
    }
    for (Choice choice : all choices) {
        if (can prune choice based on prediction) continue; // 预测性剪枝
        make choice;
        backtrack(path with choice, params);
        undo choice;
    }
}

实现回溯和剪枝的最佳实践和技巧：

细致的问题分析：仔细理解问题，明确何时可以剪枝。
合理利用数据结构：选择适合的数据结构来保存中间结果，以便高效检查约束。
灵活调整策略：根据问题的特点灵活设计剪枝策略。
递归与迭代的平衡：在某些情况下，适当使用迭代代替递归可以减少栈空间的使用。

经典例题

N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

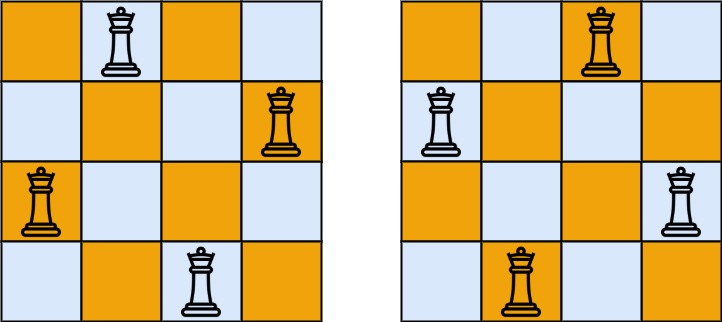
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

解题思路

n 皇后问题的核心问题是在一个 n×n 的棋盘上放置 n 个皇后，并确保它们彼此之间不在同一行、同一列或同一斜线上。由于皇后可以攻击同一行、同一列和两条对角线上的任何位置，因此需要仔细规划每个皇后的位置。

行列考虑：由于每行只能放置一个皇后，我们可以逐行放置皇后，这样可以简化问题。
深度优先搜索：使用回溯法，一种深度优先搜索（DFS）算法来逐行尝试放置皇后。
逐行放置：从第一行开始，尝试在每一列放置一个皇后。对每一行重复此操作。
合法性检查：
- 列检查：检查当前列是否已经有皇后。
- 对角线检查：检查两个方向的对角线是否已经有皇后。
回溯：如果当前位置放置皇后不合法（即在攻击范围内），则回溯（撤销当前行的选择）并尝试下一列。
记录解：每当找到一个合法位置放置完所有皇后，记录当前棋盘的布局作为一个解。

解题步骤

初始化棋盘：创建一个 n×n 的棋盘，用 . 表示空位，Q 表示皇后。
开始搜索：从第一行开始，尝试在每一列放置皇后。
合法性验证：
- 遍历之前的每一行，检查在同一列或对角线上是否已经放置了皇后。
- 如果是，尝试当前行的下一列；如果不是，则在当前位置放置皇后。
递归到下一行：当前行放置完毕后，递归到下一行。
回溯：如果在某行找不到合法位置放置皇后，回溯到上一行，改变皇后的位置。
找到解：当所有皇后都放置完毕，将当前的棋盘布局添加到解集中。
遍历所有可能：通过递归和回溯，遍历所有可能的棋盘布局，最终得到所有解。

通过这种方法，我们可以找到 n 皇后问题的所有解决方案。每种解法都是一个独特的棋盘布局，其中的皇后互不威胁。

Java题解

为了解决这个问题，我们可以使用回溯算法。下面是具体的步骤和对应的Java代码：

选择数据结构：使用一个数组 int[] queens 来记录每一行皇后的位置。queens[i] = j 表示第 i 行的皇后放在第 j 列。
检查是否安全：在放置每个皇后之前，检查该位置是否被其他皇后攻击。
递归与回溯：从第一行开始，逐行放置皇后。如果当前行的所有列都不安全，回溯到上一行，改变皇后的位置。
记录解：每当所有皇后都安全放置时，记录下当前棋盘的配置。

import java.util.ArrayList;
import java.util.List;

public class NQueens {
    public List<List<String>> solveNQueens(int n) {
        // 初始化一个 n×n 的棋盘，所有位置初始为空位 '.'
        char[][] board = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                board[i][j] = '.';
            }
        }

        // 存储所有的解决方案
        List<List<String>> solutions = new ArrayList<>();

        // 开始回溯过程，从第0行开始
        backtrack(board, 0, solutions);

        // 返回所有找到的解决方案
        return solutions;
    }

    // 回溯方法
    private void backtrack(char[][] board, int row, List<List<String>> solutions) {
        // 如果已经填满了所有行，表示找到了一个解决方案
        if (row == board.length) {
            solutions.add(createSolution(board));
            return;
        }

        // 尝试在当前行的每一列放置皇后
        for (int col = 0; col < board.length; col++) {
            // 检查在(row, col)位置放置皇后是否合法
            if (!isValid(board, row, col)) continue;

            // 放置皇后
            board[row][col] = 'Q';

            // 递归到下一行
            backtrack(board, row + 1, solutions);

            // 回溯：移除刚才放置的皇后，尝试下一个位置
            board[row][col] = '.';
        }
    }

    // 将字符数组棋盘转换成字符串列表，作为一种解决方案
    private List<String> createSolution(char[][] board) {
        List<String> solution = new ArrayList<>();
        for (char[] row : board) {
            solution.add(new String(row));
        }
        return solution;
    }

    // 检查在指定位置放置皇后是否合法
    private boolean isValid(char[][] board, int row, int col) {
        // 检查列
        for (int i = 0; i < row; i++) {
            if (board[i][col] == 'Q') {
                return false; // 在同一列发现了另一个皇后
            }
        }
        // 检查左上角斜线
        for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if (board[i][j] == 'Q') {
                return false; // 在左上角斜线发现了另一个皇后
            }
        }
        // 检查右上角斜线
        for (int i = row - 1, j = col + 1; i >= 0 && j < board.length; i--, j++) {
            if (board[i][j] == 'Q') {
                return false; // 在右上角斜线发现了另一个皇后
            }
        }
        return true; // 在所有检查中都没有发现问题，放置合法
    }

    public static void main(String[] args) {
        NQueens solution = new NQueens();
        List<List<String>> results = solution.solveNQueens(4);
        
        // 输出所有解
        for (List<String> board : results) {
            for (String row : board) {
                System.out.println(row);
            }
            System.out.println();
        }
    }
}

解数独

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例 1：

输入：

board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]

输出：

[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]

解释： 输入的数独如上图所示，唯一有效的解决方案如下所示：

编写解决数独的程序是一个经典的回溯算法应用。这个问题的核心是填充空格，同时遵守数独的三个规则。下面是解题的思路和逻辑：

解题思路

逐格尝试：遍历数独的每个格子，对于每个空白格尝试填入数字。
遵守规则：尝试填入的数字必须满足数独的规则：
- 在当前行没有重复；
- 在当前列没有重复；
- 在当前 3x3 的宫内没有重复。
回溯探索：
- 如果一个数字放在当前格子是合法的，那么继续填充下一个空白格；
- 如果填入的数字导致后续无法满足数独规则，回溯到前一个空白格，尝试另一个数字。
找到解决方案：当所有空白格都合法地填满数字后，整个数独解决。

逻辑实现

主函数：接受一个数独板作为输入，启动回溯过程。
回溯函数：
- 按行和列遍历数独板；
- 遇到空白格（‘.’），尝试填入1到9的每个数字；
- 每次填入数字后，检查是否合法，如果合法则递归地填充下一个空格；
- 如果填入数字导致后续没有合法解，撤销填入，尝试下一个数字；
- 如果找到合法解，返回 true；
合法性检查函数：检查当前行、列和3x3宫内是否有重复数字。
完成条件：所有空白格都被合法地填满。

Java题解

public class SudokuSolver {
    public void solveSudoku(char[][] board) {
        // 如果板为空或大小为0，则直接返回
        if (board == null || board.length == 0) return;
        // 调用解决方法
        solve(board);
    }

	//使用回溯算法解决数独问题
    private boolean solve(char[][] board) {
        // 遍历数独的每个格子
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                // 找到一个空格（用'.'表示）
                if (board[i][j] == '.') {
                    // 尝试填入数字1到9
                    for (char c = '1'; c <= '9'; c++) {
                        // 检查在当前位置填入数字c是否合法
                        if (isValid(board, i, j, c)) {
                            // 填入数字
                            board[i][j] = c;
                            // 递归解决下一个空格
                            if (solve(board)) {
                                return true;
                            } else {
                                // 如果填入数字c导致无法解决数独，回溯（清空此格）
                                board[i][j] = '.';
                            }
                        }
                    }
                    // 如果所有数字都无法填入此格，则回溯
                    return false;
                }
            }
        }
        // 所有格子均已正确填写，返回true
        return true;
    }

    // 检查在指定位置填入特定数字是否合法
    private boolean isValid(char[][] board, int row, int col, char c) {
        for (int i = 0; i < 9; i++) {
            // 检查同列是否有重复数字
            if (board[i][col] == c) return false;
            // 检查同行是否有重复数字
            if (board[row][i] == c) return false;
            // 检查对应3x3宫格内是否有重复数字
            if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) return false;
        }
        // 当前位置填入c是合法的
        return true;
    }
}

更多【算法-蓝桥杯第十五届抱佛脚（六）回溯与剪枝】相关视频教程：www.yxfzedu.com

算法-蓝桥杯第十五届抱佛脚（六）回溯与剪枝

蓝桥杯第十五届抱佛脚（六）回溯与剪枝

基本概念

回溯算法

回溯算法的工作原理

算法的步骤和结构框架

递归与回溯的关系

剪枝

剪枝的定义和目的

算法设计和实现

经典例题

N 皇后

解题思路

解题步骤

Java题解

解数独

解题思路

逻辑实现

Java题解

相关文章推荐

友情链接

课程目录

技术交流QQ群