算法-力扣热门算法题 135. 分发糖果，146. LRU 缓存，148. 排序链表

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例 1：
输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2：
输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

解题思路

这个问题可以通过使用贪心算法来解决。解题的关键在于确保每个孩子都至少得到一个糖果，并且在满足相邻孩子之间的评分差异时，使用尽可能少的糖果。解题步骤如下：

初始化：创建一个与 ratings 长度相同的数组 candies，初始时每个孩子都分配 1 个糖果，即 candies[i] = 1。
从左向右扫描：遍历 ratings 数组，从第二个元素开始，比较当前孩子和前一个孩子的评分。如果当前孩子的评分高于前一个孩子，那么当前孩子的糖果数应该比前一个孩子多一个，即 candies[i] = candies[i-1] + 1。
从右向左扫描：再次遍历 ratings 数组，这次是从倒数第二个元素向第一个元素遍历。比较当前孩子和后一个孩子的评分。如果当前孩子的评分高于后一个孩子，并且当前孩子的糖果数不大于后一个孩子，那么当前孩子的糖果数应该比后一个孩子多一个，即 candies[i] = max(candies[i], candies[i+1] + 1)。
计算总糖果数：最后，将 candies 数组中的所有值相加，得到的总和就是需要准备的最少糖果数目。

完整代码

Python

class Solution:
    def candy(self, ratings: List[int]) -> int:
        n = len(ratings)
        candies = [1] * n  # Step 1: Initialize

        # Step 2: Scan from left to right
        for i in range(1, n):
            if ratings[i] > ratings[i - 1]:
                candies[i] = candies[i - 1] + 1

        # Step 3: Scan from right to left
        for i in range(n - 2, -1, -1):
            if ratings[i] > ratings[i + 1]:
                candies[i] = max(candies[i], candies[i + 1] + 1)

        # Step 4: Calculate the total number of candies
        return sum(candies)

Java

public class Solution {
    public int candy(int[] ratings) {
        int n = ratings.length;
        int[] candies = new int[n];
        Arrays.fill(candies, 1);  // Step 1: Initialize

        // Step 2: Scan from left to right
        for (int i = 1; i < n; i++) {
            if (ratings[i] > ratings[i - 1]) {
                candies[i] = candies[i - 1] + 1;
            }
        }

        // Step 3: Scan from right to left
        for (int i = n - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                candies[i] = Math.max(candies[i], candies[i + 1] + 1);
            }
        }

        // Step 4: Calculate the total number of candies
        int totalCandies = 0;
        for (int candy : candies) {
            totalCandies += candy;
        }
        return totalCandies;
    }
}

146. LRU 缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

解题思路

数据结构设计：
- 定义双向链表的节点类，节点包含 key、value、prev 和 next 四个属性。
- 定义 LRUCache 类，包含 capacity、size、cache（哈希表）和两个哨兵节点 head 和 tail 来表示双向链表的头部和尾部。
辅助函数：
- addNode(Node node)：在双向链表的头部添加一个新节点。
- removeNode(Node node)：从链表中删除一个节点。
- moveToHead(Node node)：将一个存在的节点移动到双向链表的头部。
- popTail()：弹出双向链表尾部的节点，并返回该节点。
主要操作：
- LRUCache(int capacity)：初始化 LRU 缓存。
- int get(int key)：如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1。如果 key 存在，还需要将对应的节点移动到双向链表的头部。
- void put(int key, int value)：如果关键字 key 已经存在，则变更其数据值 value 并移动到双向链表的头部；如果不存在，则向缓存中插入该组 key-value。如果插入操作导致关键字数量超过 capacity，则需要从双向链表的尾部删除最久未使用的节点，并且在哈希表中删除对应的项。

完整代码

Python

class DLinkedNode():
    def __init__(self):
        self.key = 0
        self.value = 0
        self.prev = None
        self.next = None

class LRUCache:

    def _add_node(self, node):
        node.prev = self.head
        node.next = self.head.next

        self.head.next.prev = node
        self.head.next = node

    def _remove_node(self, node):
        prev = node.prev
        new = node.next

        prev.next = new
        new.prev = prev

    def _move_to_head(self, node):
        self._remove_node(node)
        self._add_node(node)

    def _pop_tail(self):
        res = self.tail.prev
        self._remove_node(res)
        return res

    def __init__(self, capacity: int):
        self.cache = {}
        self.size = 0
        self.capacity = capacity
        self.head, self.tail = DLinkedNode(), DLinkedNode()

        self.head.next = self.tail
        self.tail.prev = self.head

    def get(self, key: int) -> int:
        node = self.cache.get(key, None)
        if not node:
            return -1

        self._move_to_head(node)

        return node.value

    def put(self, key: int, value: int) -> None:
        node = self.cache.get(key)

        if not node:
            newNode = DLinkedNode()
            newNode.key = key
            newNode.value = value

            self.cache[key] = newNode
            self._add_node(newNode)

            self.size += 1

            if self.size > self.capacity:
                tail = self._pop_tail()
                del self.cache[tail.key]
                self.size -= 1
        else:
            node.value = value
            self._move_to_head(node)

Java


class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
    }

    private void addNode(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        DLinkedNode prev = node.prev;
        DLinkedNode next = node.next;
        prev.next = next;
        next.prev = prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addNode(node);
    }

    private DLinkedNode popTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }

    private HashMap<Integer, DLinkedNode> cache = new HashMap<>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }
    
    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) return -1;
        moveToHead(node);
        return node.value;
    }
    
    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);

        if (node == null) {
            DLinkedNode newNode = new DLinkedNode();
            newNode.key = key;
            newNode.value = value;

            cache.put(key, newNode);
            addNode(newNode);

            ++size;

            if (size > capacity) {
                DLinkedNode tail = popTail();
                cache.remove(tail.key);
                --size;
            }
        } else {
            node.value = value;
            moveToHead(node);
        }
    }
}

148. 排序链表

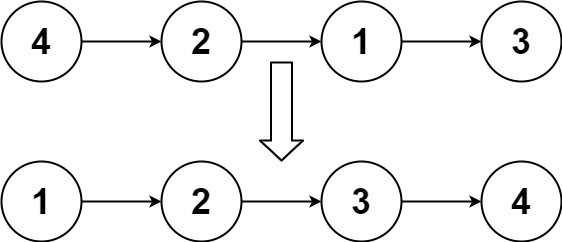
给你链表的头结点 head ，请将其按升序排列并返回 排序后的链表 。

示例 1：
输入：head = [4,2,1,3]
输出：[1,2,3,4]
示例 2：
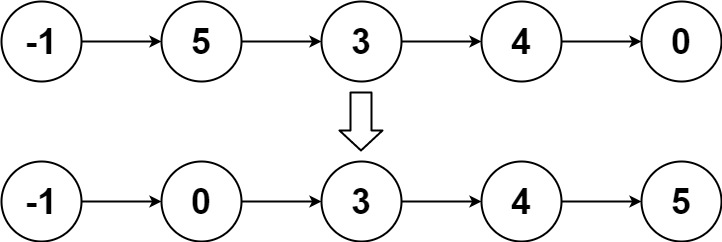
输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]
示例 3：
输入：head = []
输出：[]

解题思路

对链表进行排序可以通过多种算法来实现，其中归并排序因其稳定的 O(nlogn) 时间复杂度而广泛应用于链表排序中。链表的归并排序可以分为以下几个步骤：

寻找中点：使用快慢指针法找到链表的中点（慢指针每次前进一步，快指针每次前进两步，当快指针到达末尾时，慢指针即在中点）。
切分链表：将链表从中点处切分为两个链表，进行递归排序。
合并链表：将两个已排序的链表合并为一个有序链表。

完整代码

Python

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def sortList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        # 如果链表为空或者只有一个节点，直接返回
        if not head or not head.next:
            return head
        
        # 快慢指针找到中点
        slow, fast = head, head.next
        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        
        # 分割链表
        mid, slow.next = slow.next, None

        # 递归排序
        left, right = self.sortList(head), self.sortList(mid)

        # 合并两个有序链表
        return self.merge(left, right)

    # 合并两个有序链表的函数
    def merge(self, l1: ListNode, l2: ListNode) -> ListNode:
        dummy = tail = ListNode()
        while l1 and l2:
            if l1.val < l2.val:
                tail.next, l1 = l1, l1.next
            else:
                tail.next, l2 = l2, l2.next
            tail = tail.next
        tail.next = l1 or l2
        return dummy.next

Java

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
public class Solution {
    public ListNode sortList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        // Step 1: 寻找中点
        ListNode slow = head, fast = head.next;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }

        // Step 2: 切分链表
        ListNode mid = slow.next;
        slow.next = null;

        // Step 3: 递归排序
        ListNode left = sortList(head);
        ListNode right = sortList(mid);

        // Step 4: 合并链表
        ListNode dummy = new ListNode(0);
        ListNode tail = dummy;
        while (left != null && right != null) {
            if (left.val < right.val) {
                tail.next = left;
                left = left.next;
            } else {
                tail.next = right;
                right = right.next;
            }
            tail = tail.next;
        }
        tail.next = (left != null) ? left : right;
        return dummy.next;
    }
}

更多【算法-力扣热门算法题 135. 分发糖果，146. LRU 缓存，148. 排序链表】相关视频教程：www.yxfzedu.com

算法-力扣热门算法题 135. 分发糖果，146. LRU 缓存，148. 排序链表

135. 分发糖果

解题思路

完整代码

Python

Java

146. LRU 缓存

解题思路

完整代码

Python

Java

148. 排序链表

解题思路

完整代码

Python

Java

相关文章推荐

友情链接

课程目录

技术交流QQ群