算法-力扣热门算法题 46-48

46. 全排列，47. 全排列 II，48. 旋转图像，每题做详细思路梳理，配套Python&Java双语代码， 2024.03.19 可通过leetcode所有测试用例。

目录

46. 全排列

解题思路

完整代码

Python

Java

47. 全排列 II

解题思路

完整代码

Python

​编辑

Java

48. 旋转图像

解题思路

完整代码

Python

Java

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

解题思路

        我们可以定义一个辅助函数来实现回溯。这个函数将维护一个当前的排列path和一个记录哪些数字已被使用的used数组。每次递归时，我们遍历nums数组中的每个数字，如果这个数字尚未被使用，我们就把它添加到当前排列中，并标记为已使用，然后递归调用辅助函数。递归结束后，我们需要撤销当前数字的使用状态，以便进行下一次循环的尝试。

步骤如下：

1. 定义结果列表res来存储所有可能的全排列。
2. 定义辅助函数backtrack，它接受当前路径path和使用状态数组used。
3. 在backtrack函数中，如果path的长度等于nums的长度，说明找到了一个全排列，将其添加到res中。
4. 遍历nums数组，如果当前元素未被使用，则将其添加到path中，并标记为已使用，然后递归调用backtrack。递归返回后，撤销当前元素的使用状态和path中的元素，以进行下一轮尝试。
5. 调用backtrack函数开始回溯过程，并返回res作为所有可能的全排列。

完整代码

Python

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        def backtrack(path, used):
            # 如果当前路径的长度等于 nums 的长度，说明找到了一个全排列
            if len(path) == len(nums):
                res.append(path[:])  # 深拷贝当前路径到结果列表
                return
            for i in range(len(nums)):
                if not used[i]:  # 检查 nums[i] 是否已在当前路径中
                    path.append(nums[i])  # 添加到路径
                    used[i] = True  # 标记为已使用
                    backtrack(path, used)  # 递归
                    path.pop()  # 回溯，移除路径最后一个元素
                    used[i] = False  # 回溯，标记为未使用

        res = []  # 存储所有可能的全排列
        backtrack([], [False] * len(nums))  # 初始化路径和使用状态数组
        return res

Java

public class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        backtrack(res, nums, new ArrayList<>(), new boolean[nums.length]);
        return res;
    }

    private void backtrack(List<List<Integer>> res, int[] nums, List<Integer> path, boolean[] used) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));  // 添加一种全排列到结果列表
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (!used[i]) {
                path.add(nums[i]);  // 添加到路径
                used[i] = true;  // 标记为已使用
                backtrack(res, nums, path, used);  // 递归
                path.remove(path.size() - 1);  // 回溯，移除路径最后一个元素
                used[i] = false;  // 回溯，标记为未使用
            }
        }
    }
}

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

解题思路

解决包含重复数字序列的全排列问题，核心思路仍然是使用回溯算法，但需要额外注意如何避免生成重复的排列。为此，我们可以采取以下策略：

1. 排序：首先将数组排序，这样可以让相同的数字聚在一起，便于后续步骤中判断重复。
2. 选择路径：在遍历每个数字时，如果当前数字与前一个数字相同，并且前一个数字未被使用（说明在同一层递归中），则跳过当前数字，以避免产生重复的排列。
3. 回溯：与之前相同，通过递归调用来探索所有可能的路径，每次调用都尝试添加一个尚未被选择的数字。
4. 终止条件：当当前排列的长度等于原数组长度时，说明找到了一个全排列，将其添加到结果集中。

完整代码

Python

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        res = []
        nums.sort()  # 排序，让相同的数字聚在一起
        def backtrack(path, used):
            if len(path) == len(nums):
                res.append(path[:])
                return
            for i in range(len(nums)):
                # 如果当前数字已被使用，或者与前一个数字相同且前一个数字未被使用，则跳过
                if used[i] or (i > 0 and nums[i] == nums[i-1] and not used[i-1]):
                    continue
                used[i] = True
                path.append(nums[i])
                backtrack(path, used)
                used[i] = False
                path.pop()
        backtrack([], [False] * len(nums))
        return res

Java

public class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);  // 排序
        backtrack(res, nums, new ArrayList<>(), new boolean[nums.length]);
        return res;
    }

    private void backtrack(List<List<Integer>> res, int[] nums, List<Integer> path, boolean[] used) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (used[i] || (i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
                continue;
            }
            used[i] = true;
            path.add(nums[i]);
            backtrack(res, nums, path, used);
            used[i] = false;
            path.remove(path.size() - 1);
        }
    }
}

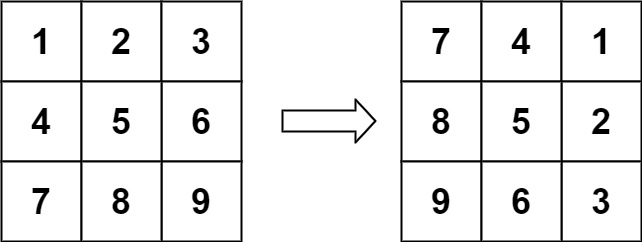
48. 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

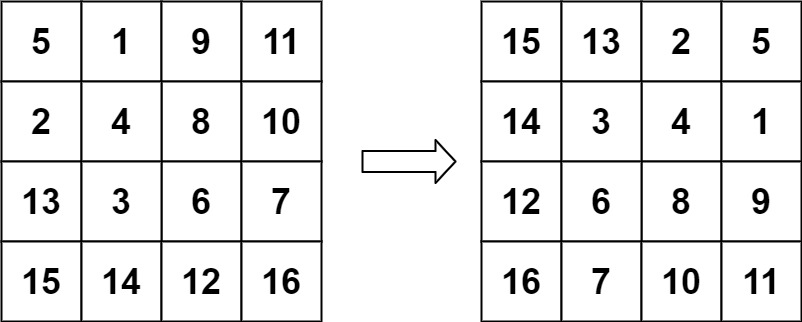
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

解题思路

将图像顺时针旋转90度，可以通过以下两步完成：

1. 转置矩阵：转置指的是将矩阵的行变成列，即matrix[i][j]变成matrix[j][i]。
2. 翻转每一行：将每一行的元素翻转，即第一个元素和最后一个元素交换，第二个元素和倒数第二个元素交换，以此类推。

详细步骤：

• 对于矩阵的每一行，我们使用一个循环交换元素，即matrix[i][j]和matrix[j][i]进行交换，这样可以得到矩阵的转置。
• 转置之后，我们对每一行进行翻转。可以通过双指针的方法来实现，即一个指针指向行的开始，另一个指针指向行的结束，交换这两个指针指向的元素，然后移动指针直到它们相遇。

完整代码

Python

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # 转置矩阵
        for i in range(n):
            for j in range(i, n):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        # 翻转每一行
        for i in range(n):
            matrix[i].reverse()

Java

public class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // 转置矩阵
        for (int i = 0; i < n; i++) {
            for (int j = i; j < n; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        // 翻转每一行
        for (int i = 0; i < n; i++) {
            for (int j = 0, k = n - 1; j < k; j++, k--) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][k];
                matrix[i][k] = temp;
            }
        }
    }
}