算法-线性代数(一)——向量基础
推荐 原创向量基础
- 1、向量和线性组合
- 2、向量的模和点乘
- 3、矩阵
- 4、参考
线性代数的核心是向量的加和乘两种运算的组合,本篇博客为线性代数的一个引子,主要从向量、线性组合和矩阵逐步引出线性代数的相关知识。
1、向量和线性组合
首先介绍的是向量相关,向量是基础。
已知列向量: υ = [ v 1 v 2 ] \boldsymbol{\upsilon}=\left[\begin{matrix} v_1 \\ v_2\end{matrix} \right] υ=[v1v2], ω = [ w 1 w 2 ] \boldsymbol{\omega}=\left[\begin{matrix} w_1 \\ w_2\end{matrix} \right] ω=[w1w2];
向量加法: υ + ω = [ v 1 + w 1 v 2 + w 2 ] \boldsymbol{\upsilon}+\boldsymbol{\omega}=\left[\begin{matrix} v_1+w_1 \\ v_2+w_2\end{matrix} \right] υ+ω=[v1+w1v2+w2];
纯量乘法: c υ = [ c v 1 c v 2 ] c\boldsymbol{\upsilon}=\left[\begin{matrix} cv_1 \\ cv_2\end{matrix} \right] cυ=[cv1cv2], c c c是标量;
线性组合:我们将 υ \boldsymbol{\upsilon} υ和 ω \boldsymbol{\omega} ω的加法运算和标量乘法运算结合起来,得到的结果称为 υ \boldsymbol{\upsilon} υ和 ω \boldsymbol{\omega} ω的线性组合,即 c υ + d ω c\boldsymbol{\upsilon}+d\boldsymbol{\omega} cυ+dω。
两个向量的线性组合就是线性代数的最简单的形式。
下图展示了向量加法的结果:
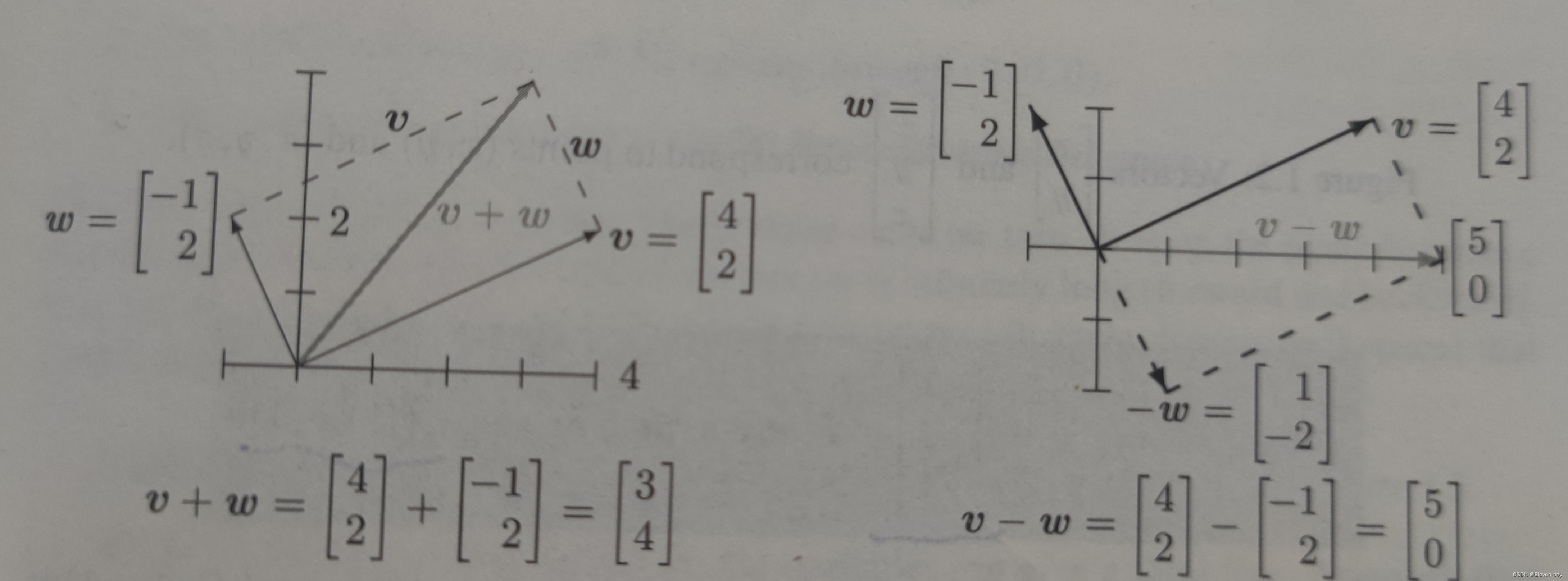
Tip:列向量 υ = [ a b c ] \boldsymbol{\upsilon}=\left[\begin{matrix} a \\ b \\ c\end{matrix} \right] υ=⎣⎡abc⎦⎤也可以写为 υ = ( a , b , c ) \boldsymbol{\upsilon}=( a , b , c ) υ=(a,b,c),这两种形式都是表示列向量,后一种可以节约书写空间。另外,行向量表示为 υ = [ a , b , c ] \boldsymbol{\upsilon}=[ a , b , c ] υ=[a,b,c],平躺着并用方括号表示。
2、向量的模和点乘
点乘(内积):点乘为两个向量对应位置上元素乘积的和。
向量 υ = ( v 1 , v 2 , v 3 , . . . , v n ) \boldsymbol{\upsilon}=( v_1 , v_2 , v_3,...,v_n ) υ=(v1,v2,v3,...,vn)和向量 ω = ( w 1 , w 2 , w 3 , . . . , w n ) \boldsymbol{\omega}=( w_1 , w_2 , w_3,...,w_n ) ω=(w1,w2,w3,...,wn)的点乘表示为:
υ ⋅ ω = v 1 w 1 + v 2 w 2 + . . . + v n w n \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}=v_1w_1+v_2w_2+...+v_nw_n υ⋅ω=v1w1+v2w2+...+vnwn
向量 υ = ( v 1 , v 2 , v 3 , . . . , v n ) \boldsymbol{\upsilon}=( v_1 , v_2 , v_3,...,v_n ) υ=(v1,v2,v3,...,vn)和其自身的点乘为:
υ ⋅ υ = v 1 2 + v 2 2 + . . . + v n 2 = ( v 1 − 0 ) 2 + ( v 2 − 0 ) 2 + . . . + ( v n − 0 ) 2 \boldsymbol{\upsilon} \cdot \boldsymbol{\upsilon}=v^2_1+v^2_2+...+v^2_n=(v_1-0)^2+(v_2-0)^2+...+(v_n-0)^2 υ⋅υ=v12+v22+...+vn2=(v1−0)2+(v2−0)2+...+(vn−0)2
向量的长度(模)
则在 n n n维坐标系中, υ ⋅ υ \boldsymbol{\upsilon} \cdot \boldsymbol{\upsilon} υ⋅υ表示点 ( v 1 , v 2 , v 3 , . . . , v n ) ( v_1 , v_2 , v_3,...,v_n) (v1,v2,v3,...,vn)到坐标原点的距离的平方,即向量 υ \boldsymbol{\upsilon} υ的长度的平方,所以向量 υ \boldsymbol{\upsilon} υ的长度为:
l e n g t h = ∥ υ ∥ = υ ⋅ υ = ( v 1 2 + v 2 2 + . . . + v n 2 ) 1 / 2 \mathbf{length}= \left \|\boldsymbol{\upsilon}\right\|=\sqrt{\boldsymbol{\upsilon} \cdot \boldsymbol{\upsilon}}=(v^2_1+v^2_2+...+v^2_n)^{1/2} length=∥υ∥=υ⋅υ=(v12+v22+...+vn2)1/2
如下图所示:
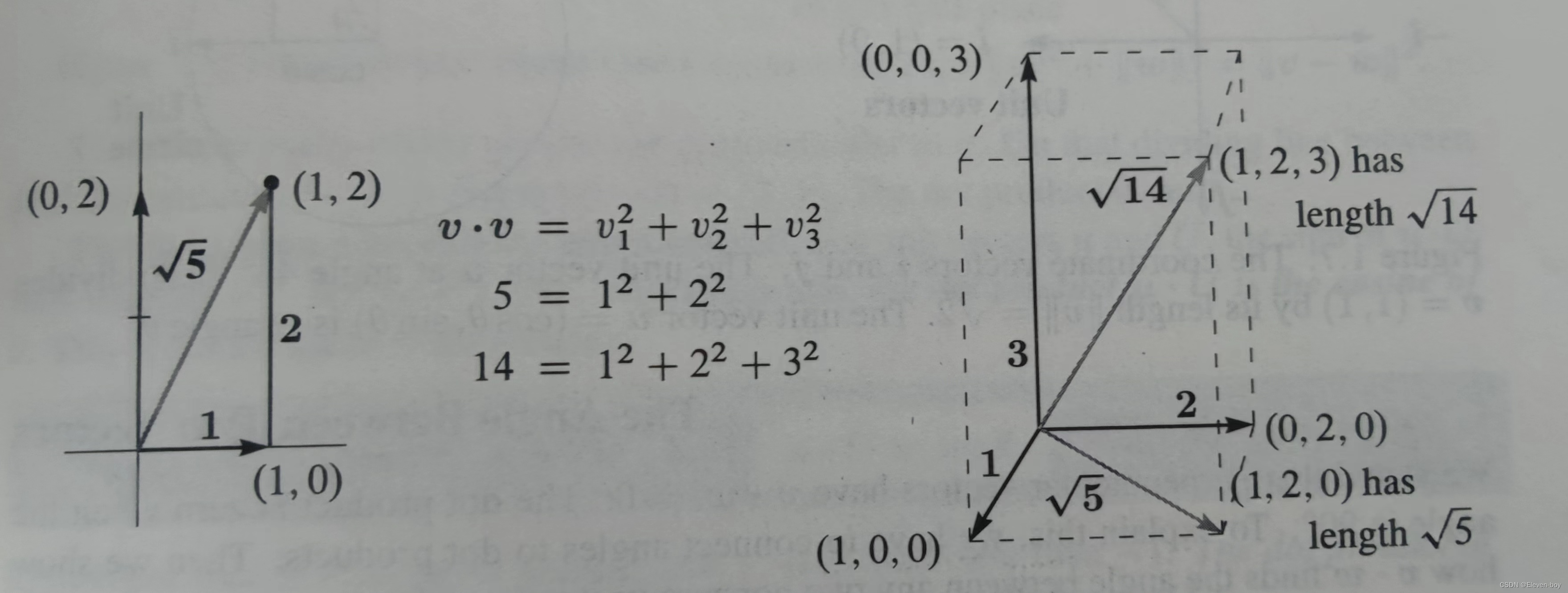
单位向量
单位向量是长度等于1的向量,则向量 υ \boldsymbol{\upsilon} υ的单位向量 u \boldsymbol{u} u为任何非零向量除以该向量的长度,即:
u = υ ∥ υ ∥ \boldsymbol{u}=\frac{\boldsymbol{\upsilon}}{ \left \|\boldsymbol{\upsilon}\right\|} u=∥υ∥υ
下图为单位向量的示意图:
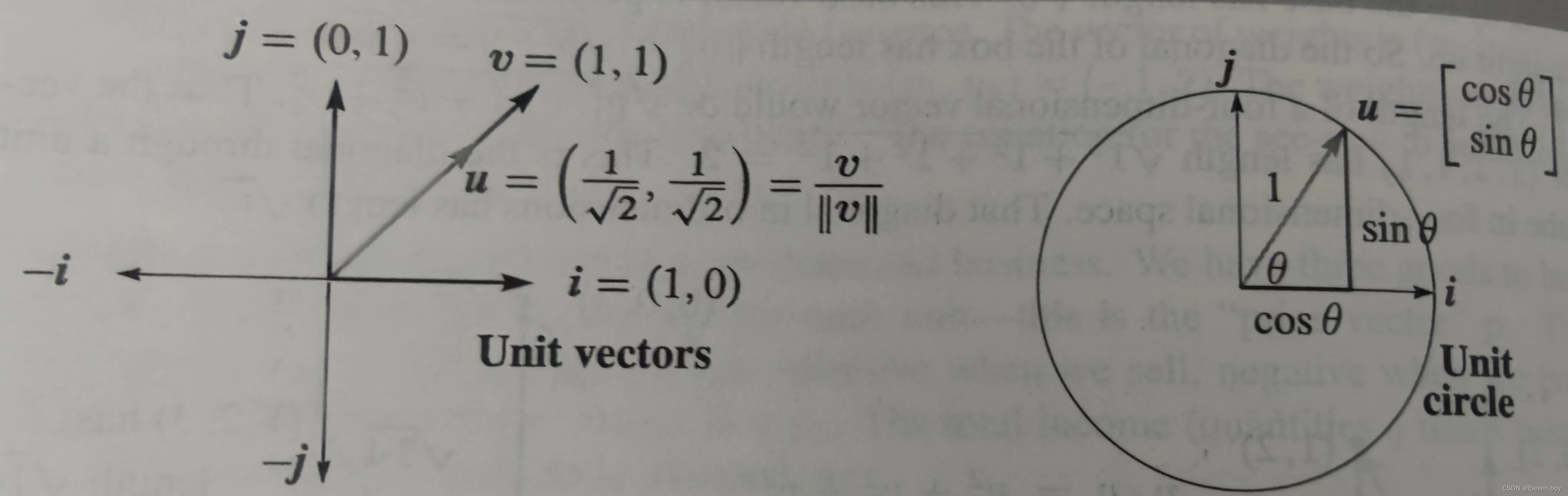
对于非零向量,当向量 υ \boldsymbol{\upsilon} υ垂直向量 ω \boldsymbol{\omega} ω时,它们的点积为零,即:
υ ⋅ ω = 0 \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}=0 υ⋅ω=0
可结合勾股定理进行证明。
向量夹角
设向量 υ \boldsymbol{\upsilon} υ和向量 ω \boldsymbol{\omega} ω的夹角为 θ \theta θ,当 υ ⋅ ω ! = 0 \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}!=0 υ⋅ω!=0时,会有:
{ θ < 9 0 ∘ , υ ⋅ ω > 0 θ > 9 0 ∘ , υ ⋅ ω < 0 \left\{\begin{array}{cc} \theta<90^{\circ}, & \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}>0\\ \theta>90^{\circ}, & \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}<0 \end{array}\right. {
θ<90∘,θ>90∘,υ⋅ω>0υ⋅ω<0
除此之外,两个单位向量的点乘也表示两个向量夹角 θ \theta θ的 c o s i n e cosine cosine余弦值:
u ⋅ U = c o s θ , u ⋅ U ≤ 1 \boldsymbol{u} \cdot \boldsymbol{U}=cos{\theta},\boldsymbol{u} \cdot \boldsymbol{U}\leq1 u⋅U=cosθ,u⋅U≤1

那么对于非单位向量的向量 υ \boldsymbol{\upsilon} υ和向量 ω \boldsymbol{\omega} ω的夹角的余弦值应该怎么表示?
综上所述,应该为这两个向量对应的单位向量的点乘,即:
c o s θ = ( υ ∥ υ ∥ ) ⋅ ( ω ∥ ω ∥ ) = υ ⋅ ω ∥ υ ∥ ∥ ω ∥ ≤ 1 cos\theta = (\frac{\boldsymbol{\upsilon}}{\left \|\boldsymbol{\upsilon}\right\|}) \cdot (\frac{\boldsymbol{\omega}}{\left \|\boldsymbol{\omega}\right\|})=\frac{\boldsymbol{\upsilon} \cdot \boldsymbol{\omega}}{\left \|\boldsymbol{\upsilon}\right\|\left \|\boldsymbol{\omega}\right\|}\leq1 cosθ=(∥υ∥υ)⋅(∥ω∥ω)=∥υ∥∥ω∥υ⋅ω≤1
由此可引出两个著名的不等式:
柯西-施瓦兹-布尼亚科夫斯基不等式 ∣ υ ⋅ ω ∣ ≤ ∥ υ ∥ ∥ ω ∥ | \boldsymbol{\upsilon} \cdot \boldsymbol{\omega}|\leq{\left \|\boldsymbol{\upsilon}\right\|\left \|\boldsymbol{\omega}\right\|} ∣υ⋅ω∣≤∥υ∥∥ω∥
三角不等式: ∥ υ + ω ∥ ≤ ∥ υ ∥ + ∥ ω ∥ {\left \|\boldsymbol{\upsilon}+\boldsymbol{\omega}\right\|}\leq{\left \|\boldsymbol{\upsilon}\right\|+\left \|\boldsymbol{\omega}\right\|} ∥υ+ω∥≤∥υ∥+∥ω∥
3、矩阵
接下来,我们从向量过度到矩阵,用矩阵表示线性组合。前面介绍了向量之间的运算,那么当一个矩阵乘以一个向量应如何去理解呢?
首先给定三个向量:
u = [ 1 − 1 0 ] , υ = [ 0 1 − 1 ] , ω = [ 0 0 1 ] . \boldsymbol{u}=\left[\begin{matrix} 1 \\ -1 \\ 0\end{matrix} \right],\boldsymbol{\upsilon}=\left[\begin{matrix} 0 \\ 1 \\ -1\end{matrix} \right],\boldsymbol{\omega}=\left[\begin{matrix} 0 \\ 0 \\ 1\end{matrix} \right]. u=⎣⎡1−10⎦⎤,υ=⎣⎡01−1⎦⎤,ω=⎣⎡001⎦⎤.
则这三个三维向量的线性组合为: x 1 u + x 2 υ + x 3 ω x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega} x1u+x2υ+x3ω,即:
x 1 [ 1 − 1 0 ] + x 2 [ 0 1 − 1 ] + x 3 [ 0 0 1 ] = [ x 1 x 2 − x 1 x 3 − x 2 ] x_1\left[\begin{matrix} 1 \\ -1 \\ 0\end{matrix} \right]+x_2\left[\begin{matrix} 0 \\ 1 \\ -1\end{matrix} \right]+x_3\left[\begin{matrix} 0 \\ 0 \\ 1\end{matrix} \right]=\left[\begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2\end{matrix} \right] x1⎣⎡1−10⎦⎤+x2⎣⎡01−1⎦⎤+x3⎣⎡001⎦⎤=⎣⎡x1x2−x1x3−x2⎦⎤
那么用矩阵重写上面的线性组合为:
A x = [ 1 0 0 − 1 1 0 0 − 1 1 ] [ x 1 x 2 x 3 ] = [ x 1 x 2 − x 1 x 3 − x 2 ] = [ b 1 b 2 b 3 ] = b A\boldsymbol{x}=\left[\begin{matrix} 1 & 0 & 0\\ -1 & 1 & 0\\ 0 & -1 & 1\end{matrix} \right]\left[\begin{matrix} x_1 \\ x_2 \\ x_3\end{matrix} \right]=\left[\begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2\end{matrix} \right]=\left[\begin{matrix} b_1 \\ b_2 \\ b_3\end{matrix} \right]=\boldsymbol{b} Ax=⎣⎡1−1001−1001⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡x1x2−x1x3−x2⎦⎤=⎣⎡b1b2b3⎦⎤=b
从以上两式可以看出,矩阵A乘以向量 x \boldsymbol{x} x等同于矩阵 A A A的三个列向量的线性组合 x 1 u + x 2 υ + x 3 ω x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega} x1u+x2υ+x3ω,即 A x A\boldsymbol{x} Ax的结果就是矩阵A的各列的线性组合。
此外,我们也可以使用行的点乘来计算 A x A\boldsymbol{x} Ax:
A x = [ 1 0 0 − 1 1 0 0 − 1 1 ] [ x 1 x 2 x 3 ] = [ ( 1 , 0 , 0 ) ⋅ ( x 1 , x 2 , x 3 ) ( − 1 , 1 , 0 ) ⋅ ( x 1 , x 2 , x 3 ) ( 0 , − 1 , 1 ) ⋅ ( x 1 , x 2 , x 3 ) ] = [ x 1 x 2 − x 1 x 3 − x 2 ] = [ b 1 b 2 b 3 ] = b A\boldsymbol{x}=\left[\begin{matrix} 1 & 0 & 0\\ -1 & 1 & 0\\ 0 & -1 & 1\end{matrix} \right]\left[\begin{matrix} x_1 \\ x_2 \\ x_3\end{matrix} \right]=\left[\begin{matrix} (1,0,0) \cdot (x_1,x_2,x_3) \\ (-1,1,0) \cdot (x_1,x_2,x_3) \\ (0,-1,1) \cdot (x_1,x_2,x_3)\end{matrix} \right]=\left[\begin{matrix} x_1 \\ x_2-x_1 \\ x_3-x_2\end{matrix} \right]=\left[\begin{matrix} b_1 \\ b_2 \\ b_3\end{matrix} \right]=\boldsymbol{b} Ax=⎣⎡1−1001−1001⎦⎤⎣⎡x1x2x3⎦⎤=⎣⎡(1,0,0)⋅(x1,x2,x3)(−1,1,0)⋅(x1,x2,x3)(0,−1,1)⋅(x1,x2,x3)⎦⎤=⎣⎡x1x2−x1x3−x2⎦⎤=⎣⎡b1b2b3⎦⎤=b
线性等式
前面我们是已知 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,来计算等号右侧的 b \boldsymbol{b} b,那么,如果已知等号右侧的 b \boldsymbol{b} b,如何来求 x \boldsymbol{x} x呢?
旧问题: 计算线性组合 x 1 u + x 2 υ + x 3 ω x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega} x1u+x2υ+x3ω为了得出 b \boldsymbol{b} b;
新问题: u , υ , ω \boldsymbol{u},\boldsymbol{\upsilon},\boldsymbol{\omega} u,υ,ω的哪种组合可以生成指定的 b \boldsymbol{b} b。
很明显,这是一个互逆的问题。将等式 A x = b A\boldsymbol{x}=\boldsymbol{b} Ax=b改写成我们熟悉的方程式组为:
{ x 1 = b 1 − x 1 + x 2 = b 2 − x 2 + x 3 = b 3 \begin{cases} x_1&&&&&=&b_1&\\ -x_1&+&x_2&&&=&b_2& \\ &-&x_2&+&x_3&=&b_3 \end{cases} ⎩⎪⎨⎪⎧x1−x1+−x2x2+x3===b1b2b3
可轻易对该方程组求解:
{ x 1 = b 1 x 2 = b 1 + b 2 x 3 = b 1 + b 2 + b 3 \begin{cases} x_1=&b_1&\\ x_2=&b_1&+&b_2& \\ x_3=&b_1&+&b_2&+&b_3& \end{cases} ⎩⎪⎨⎪⎧x1=x2=x3=b1b1b1++b2b2+b3
写成矩阵形式为: x = A − 1 b \boldsymbol{x}=A^{-1}\boldsymbol{b} x=A−1b,我们将 A − 1 A^{-1} A−1称作 A A A的逆矩阵,此时的 A A A为可逆矩阵。
多个向量的独立和非独立性
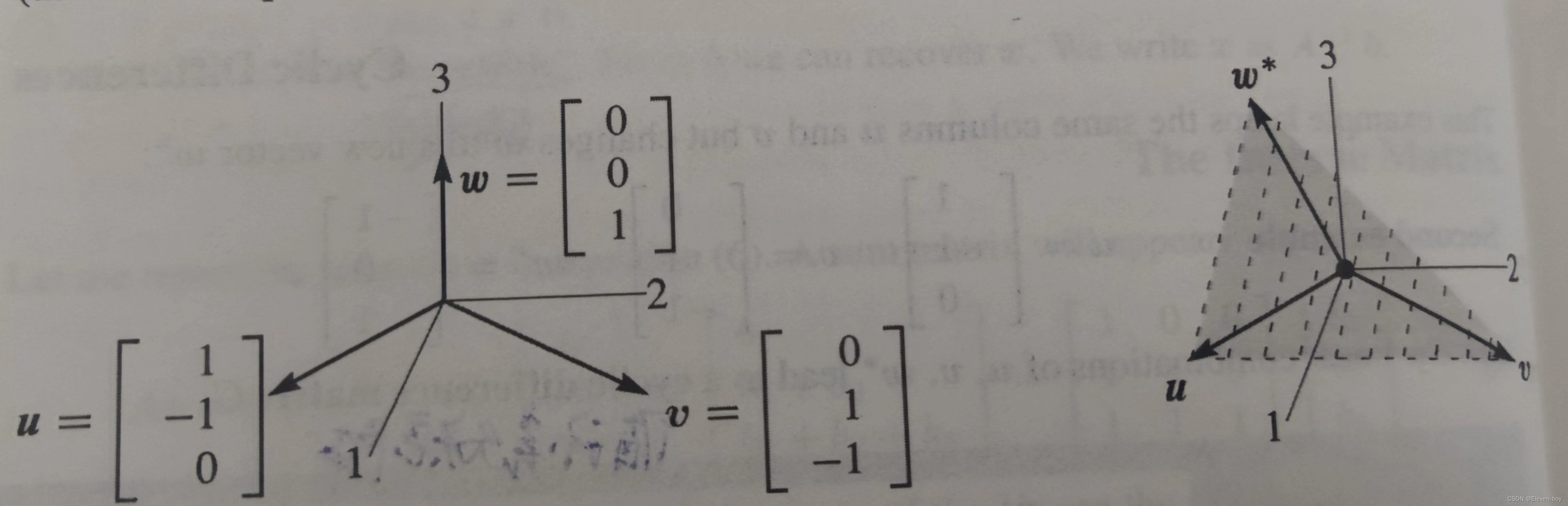
如上图所示,左右两个坐标系里向量 u 、 υ \boldsymbol{u}、\boldsymbol{\upsilon} u、υ是一样的,这两个向量的线性组合构成一个同样的二维平面,关键问题是第三个向量是否在这个平面里:
独立性: ω \boldsymbol{\omega} ω不在 u 、 υ \boldsymbol{u}、\boldsymbol{\upsilon} u、υ构成的平面中,即:
只有当 x 1 = 0 , x 2 = 0 、 x 3 = 0 x_1=0,x_2=0、x_3=0 x1=0,x2=0、x3=0时,才满足等式 x 1 u + x 2 υ + x 3 ω = 0 x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega}=\boldsymbol{0} x1u+x2υ+x3ω=0
如果矩阵 A A A的列是独立的,则 A x = 0 A\boldsymbol{x}=\boldsymbol{0} Ax=0只有一个解, A A A被称作可逆矩阵(非奇异矩阵)。
非独立性: ω ∗ \boldsymbol{\omega^*} ω∗在 u 、 υ \boldsymbol{u}、\boldsymbol{\upsilon} u、υ构成的平面中,即:
存在多组 x 1 , x 2 , x 3 x_1,x_2,x_3 x1,x2,x3,满足 x 1 u + x 2 υ + x 3 ω ∗ = 0 x_1\boldsymbol{u}+x_2\boldsymbol{\upsilon}+x_3\boldsymbol{\omega^*}=\boldsymbol{0} x1u+x2υ+x3ω∗=0
如果矩阵 C C C的列是非独立的,则 C x = 0 C\boldsymbol{x}=\boldsymbol{0} Cx=0存在多个解,矩阵 C C C被称作奇异矩阵。
4、参考
[1] Introduction Linear Algebra,Fifth Edition,Giibert Strang.
更多【算法-线性代数(一)——向量基础】相关视频教程:www.yxfzedu.com
相关文章推荐
- java-Maven的总结 - 其他
- 学习-【Azure 架构师学习笔记】-Azure Storage Account(5)- Data Lake layers - 其他
- 人工智能-高校为什么需要大数据挖掘平台? - 其他
- 数码相机-立体相机标定 - 其他
- java-java计算 - 其他
- python-前端面试题 - 其他
- git-IntelliJ IDEA 2023.2.1 (Ultimate Edition) 版本 Git 如何合并多次的本地提交进行 Push - 其他
- 音视频-中文编程软件视频推荐,自学编程电脑推荐,中文编程开发语言工具下载 - 其他
- node.js-npm install:sill idealTree buildDeps - 其他
- 编辑器-vscode 访问本地或者远程docker环境 - 其他
- git-IntelliJ IDEA 2023.2.1 (Ultimate Edition) 版本 Git 如何找回被 Drop Commit 的提交记录 - 其他
- 算法-力扣第1035题 不相交的线中等 c++ (最长公共子序列) 动态规划 附Java代码 - 其他
- java-JavaWeb课程复习资料——idea创建JDBC - 其他
- python-Python---列表的循环遍历,嵌套 - 其他
- python-Python的版本如何查询? - 其他
- java-IDEA 函数下边出现红色的波浪线,提示报错 - 其他
- 算法-算法通关村第八关|白银|二叉树的深度和高度问题【持续更新】 - 其他
- 算法-C现代方法(第19章)笔记——程序设计 - 其他
- git-IntelliJ Idea 撤回git已经push的操作 - 其他
- c#-html导出word - 其他
2):严禁色情、血腥、暴力
3):严禁发布任何形式的广告贴
4):严禁发表关于中国的政治类话题
5):严格遵守中国互联网法律法规
6):有侵权,疑问可发邮件至service@yxfzedu.com
