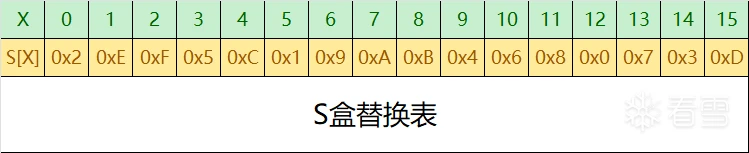
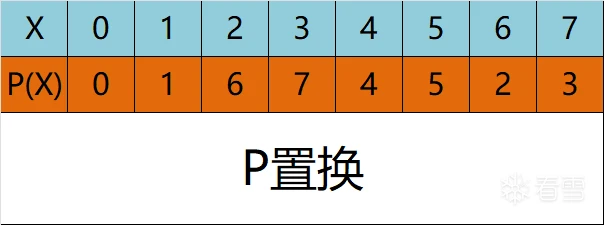
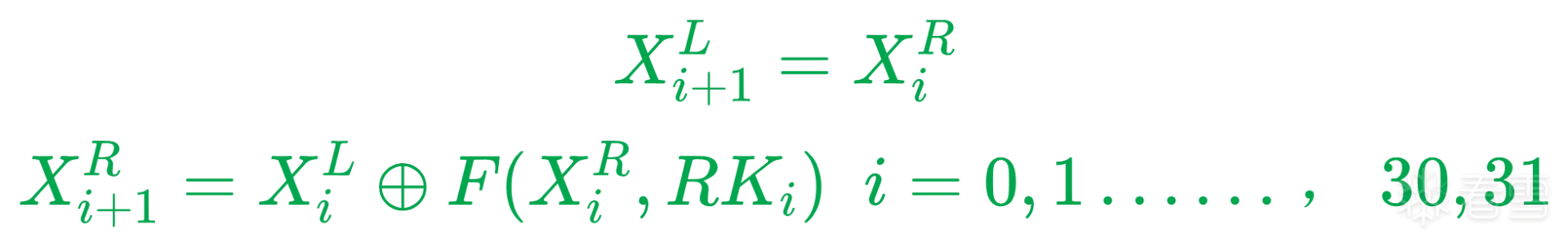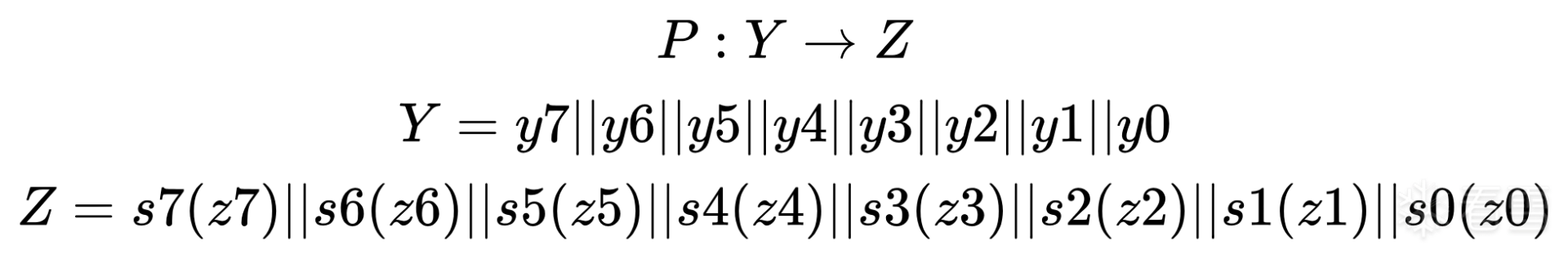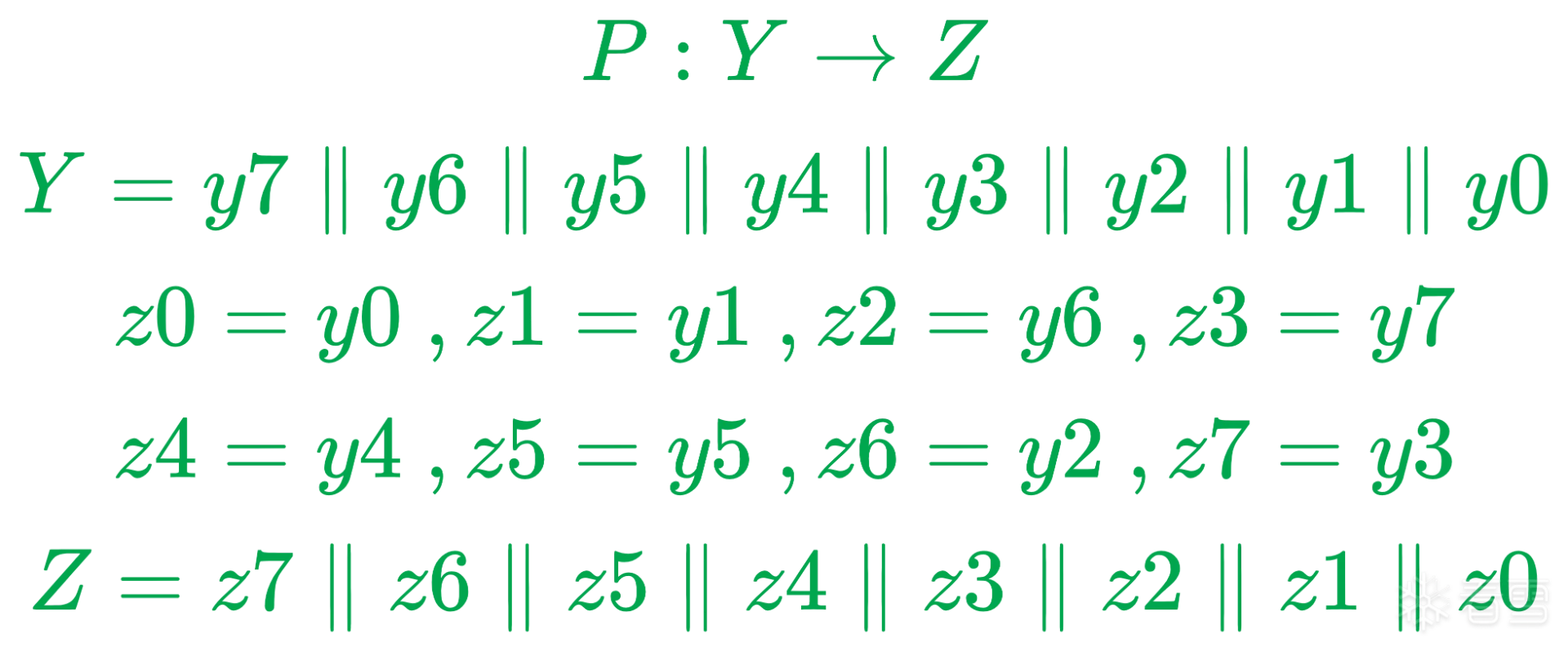密码应用-轻量级分组加密算法FeW
推荐 原创更多【密码应用-轻量级分组加密算法FeW】相关视频教程:www.yxfzedu.com
相关文章推荐
- [驱动出租]-键鼠驱动 - 游戏逆向 软件逆向 Windows内核 驱动出租
- [驱动出租]-无痕注入 - 游戏逆向 软件逆向 Windows内核 驱动出租
- CE图标工具 - 游戏逆向 软件逆向 Windows内核 驱动出租
- 驱动出租及驱动定制价格 - 游戏逆向 软件逆向 Windows内核 驱动出租
- Android安全-Lsposed 技术原理探讨 && 基本安装使用 - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-WinCHM 再探索! - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-DTrace 研究 - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-常见语言基础逆向方法合集 - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-分享个东西,cheat engine的变速精灵(speedhack)模块调用方法. - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-SoftAny WinCHM 5.496 注册码笔记 by ZeNiX - 游戏基址 二进制漏洞 密码应用 智能设备
- CTF对抗-crackme001 Acid burn - 游戏基址 二进制漏洞 密码应用 智能设备
- Android安全-定制bcc/ebpf在android平台上实现基于dwarf的用户态栈回溯 - 游戏基址 二进制漏洞 密码应用 智能设备
- CTF对抗-Java安全小白的入门心得 - 初见RMI协议 - 游戏基址 二进制漏洞 密码应用 智能设备
- 编程技术-这个崩溃有点意思,你中过招吗 - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-PE头解析-字段说明 - 游戏基址 二进制漏洞 密码应用 智能设备
- 软件逆向-PE加载过程 FileBuffer-ImageBuffer - 游戏基址 二进制漏洞 密码应用 智能设备
- 加壳脱壳-进程 Dump & PE unpacking & IAT 修复 - Windows 篇 - 游戏基址 二进制漏洞 密码应用 智能设备
- CTF对抗-第五空间 crackme深度分析 - 游戏基址 二进制漏洞 密码应用 智能设备
- Pwn-DAS9月月赛PWN题出题心路 - 游戏基址 二进制漏洞 密码应用 智能设备
- CTF对抗-CSAW-CTF-Web部分题目 - 游戏基址 二进制漏洞 密码应用 智能设备
记录自己的技术轨迹
文章规则:
1):文章标题请尽量与文章内容相符
2):严禁色情、血腥、暴力
3):严禁发布任何形式的广告贴
4):严禁发表关于中国的政治类话题
5):严格遵守中国互联网法律法规
6):有侵权,疑问可发邮件至service@yxfzedu.com
近期原创 更多