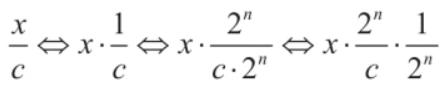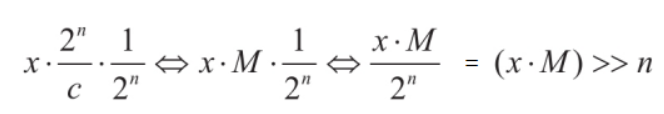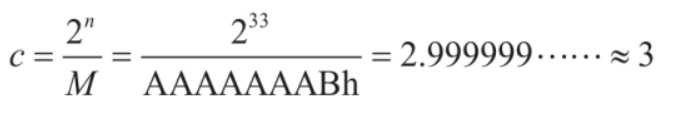序言

在学习 Andorid 逆向的过程中，发现无论是哪种编译器，生成哪个平台的代码，其优化思路在本质上如出一辙，在 Windwos 平台所使用的技巧，在安卓平台仍然适用，不外乎乘法除法计算的优化，swtich 判定树的优化，对 if 条件句的优化，while 循环的优化等等，编写本文的目的也就是为了对已学的知识进行总结。

这里强烈推荐老钱和老张写的《C++反汇编与逆向分析技术揭秘》，本文大部分知识点都将以此书作为参考，我个人是不太喜欢看直播和视屏教程的，因为有些关键知识点可能老师一句话就带过去了，要想回来看还得来回拉进度条，但是书不一样，遇到读不懂的地方可以停下来仔细思考，想回头看也就是翻几页的事情，遇到那种写的特别细的作者，那读起来更是一种享受。

本文列举的代码和汇编只是为了更好的说明思路，并不代表实际代码，好了话不多说，进入正题。

优化方向

• 编译速度优化

• 执行速度优化

• 程序体积优化

对于 Debug 版程序，编译器为了满足单步调试需求，不会对无意义的代码进行优化

无意义的意思是没有发生传递，没有赋值到内存空间

常见的优化类型

常量折叠

更像是预处理，编译器会将所有可预见的值直接写成立即数

int n = 2 + 3 * 6;
// 编译器在处理这段代码时会直接将变量赋予立即数+
// mov n, 20

常量传播

是常量折叠的“进阶版”，编译器会扫描整个代码段，对所有非变量运算直接计算出结果

int n = 2 + 3 * 6;
int m = n * 10;
// mov m, 200

减少变量

未使用即是无意义，无意义的代码都会被优化，上述的两个示例，在实际编译中是会直接被优化掉的，因为并未被用于函数传参和其他操作

编译虽然能通过，但不会产生任何代码，因为没有传递结果，对后续的代码执行不会造成任何影响

int funtion1() {
    int n = 2 + 3 * 6;
    int m = n * 10;
    return 0;
}
// 无意义的变量，这个函数被编译为汇编也将只有一句代码
// mov eax, 0
 
int funtion2() {
    int n = 2 + 3 * 6;
    int m = n * 10;
    return m;
}
// 有意义的变量，但因为常量传播，也只有一句代码
// mov eax, 200

分支优化

对于所有不可达的分支也会直接被裁剪

if(false) {
    printf("you can't find me");
}

在书中还有更多优化示例，这里不做过多列举，其根本就是以上几种优化方式，无意义的代码将被删除，冗余的代码将会被精简，照着这种思路想就对了。得益于编译器的强大，使得再烂的代码也能保持高效

数学计算上对算法的优化

我将会穿插使用 x86 和 arm 汇编，主要指令都大差不差，理解意义即可

加法

加法没有任何优化空间，一个 add 指令所需的 cpu 周期本就很短，除了上述的常量折叠外，一般不会对其进行改动

减法

理论上加法和减法的指令周期是一致的，也不排除有些编译器会将减数转成补码进行相加，遇到补码也能一眼看出来，直接就可以认定这条指令为减法

乘法

变量乘常量

• 常量为2的幂

乘法将会被替换为执行周期更短的移位指令

int fun(int n) {
    return n * 16;
}
// mov eax, n
// shl eax, 4

• 常量为非2的幂

因为 thumb 和 x86 指令集的差异，安卓平台上处理的更好一些

我并不推荐你把自己当成编译器，看到算式想着怎么转成汇编，而是推荐记下这种算法，看到计算过程知道怎么转成原式，当然也不追求100%还原，逻辑一致即可

编译器会对非2的幂进行拆解，例如：

• n * 15 = n * 16 - n = n << 4 - n

• n * 12 = n * 3 * 4 = (n << 1 + n) << 2

int value = n * 15;
// rsb.w r0, r1, r1, lsl #4

int value = n * 12;
// add.w r0, r1, r1, lsl #1

当然 windows 平台也不是一无是处，某些乘法会通过 lea 将两条指令合并成一条

• n * 4 + 5 = lea edx, [ecx * 4 + 5]

printf("%d", n * 4 + 5);
// mov ecx, n
// lea edx, [ecx * 4 + 5]
// push edx

至于值为不可拆分的素数，就改用 mul 指令

变量乘变量

这一步没有什么优化空间，因为都是未知的，只能老老实实用 mul 指令

int fun(int n, int m) {
    return n * m;
}
// mov eax, n
// mov ecx, m
// imul ecx

除法

在看下面内容之前，不妨再问问自己，真的了解除法吗？除法的本质是什么？

okok，现在是复习时间，简单总结一下以下两个问题

• 符号问题

1. 两个无符号整数相除，结果依然是无符号

2. 两个有符号整数相除，结果依然是有符号

3. 混除，参数全被当成无符号计算，结果是无符号
   

• 取整问题

1. 向下取整 —— floor 函数    存在误差 => ( - a / b ) + ( a / b ) != - ( a / b ) - ( a / b )

2. 向上取整 —— ceil 函数      存在误差 => ( - a / b ) != - ( a / b )

3. 向零取整 —— 截断除法(Truncate)，可以理解为放弃小数部分，只取整数部分，可以在任何情况保持恒等，大部分语言用的都是截断除法

除数为无符号数

• 大数（负数）

在无符号中，负数的值是很大的，例如 -8 = 0xFFFFFFF8

而除以这种大数，只能出现两种情况，1或 0，换个思路来想就可以写成这样：[被除数] >= [除数] ? 1 : 0  

我们来看看 thumb 下是怎么优化的

UINT value = (UINT)n / -8;
// cmn.w r0, #9    ; cmp r0, -9
// it hi
// movhi r1, #1    ; n > -9 ? 1 : 0

他这里做了一个小小的变形：[被除数] > [除数 - 1] ? 1 : 0，逻辑上仍然成立

• 2的幂

简单的移位

UINT value = (UINT)n / 4;
// lsrs r1, r0, #2

• 非2的幂

接下来就要引入一个非常魔幻的设定，magic number。说来这个魔数，依稀记得早在几年前的知乎上看到过一篇文章，讲的是雷神之锤游戏引擎就使用了这么一个魔数，那时的cpu是非常低效的，而为了避免使用除法这种 cpu 周期偏长的指令，天才的程序员们想出了各种奇技淫巧，其中最为后人津津乐道的就是游戏中对平方根倒数的优化，将计算过程等价替换为加法和移位操作，损失少量的精度来换取绝对的性能。

我们这里的魔数稍有不同，它是用来优化除法的，而且逻辑上也相对容易理解一些，废话不多说，进入正题。

对于普通除法，我们可以得到以下的换算：（x => 被除数变量，c => 除数常量，M => 魔数）

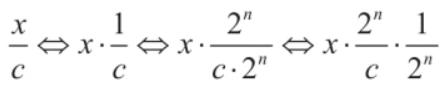
假设用 M 代替 2^n / c 这个 Magic 变量，于是有：

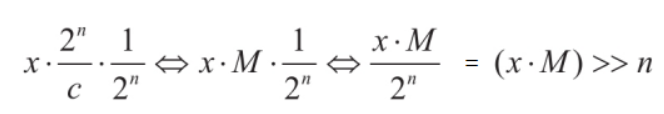
也就是说，除法将会被转会成 (x * M) >> n 的逻辑进行运算，至于 M 和 n 值怎么来的，我们不关心，这是编译器根据除数算出来的最优值，会尽力保证偏差达到最小，我们要做的是认出魔数和移了多少位，然后根据 m = 2^n/c 公式求得原本的除数 c = 2^n/m

公式来源于《C++反汇编与逆向分析技术揭秘》，真的是非常非常的细，书中整个推导过程很完整，很建议各位去仔细研读一遍

以下代码为例：

printf("%u", (unsigned)argc / 3);
// mov eax, 0xAAAAAAAB   ; M
// mul [argc]            ; edx:eax = argc * M
// shr edx, 1            ; edx = argc * M >> 32 >> 1
// push edx

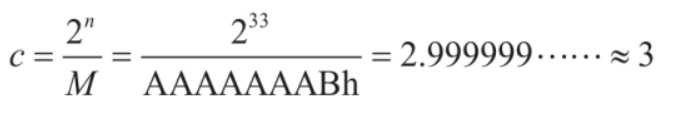
今天先写到这，还未完工，存在错误还请在评论区指正，这个属于总结篇，windows篇可以先看我以前的笔记：https://note.youdao.com/s/5tc2zdgo