Canvas is not supported in your browser.
首页 课程 文章
无痕注入 APC注入 线程注入 读写驱动 注入技术 句柄表 进程线程 系统调用 保护模式 内存管理 远程CALL 软件调试 驱动封装 云下发 驱动开发 FPS数据 方框透视 FPS方框 FPS自瞄 CE D3DHOOK D3D绘制 Imgui绘制 DWM
内核课程 驱动出租 学习路线 聊天室 免责声明 提问技巧

密码应用-白盒AES算法详解(二)

推荐 原创

周杰伦

文章分类 密码应用 阅读数 : 64 阅读时长 : 9分钟


【密码应用-白盒AES算法详解(二)】此文章归类为：密码应用。

上篇文章我们分析了AES的具体实现，并且从理论原理以及数理方向一步步进行了DFA攻击的实现，接下来这篇文章我们从实践出发，探索针对白盒算法如何快速侦破。

一、 工具选择

工欲善其事，必先利其器，通过上篇文章虽然我们可以逐步去实现DFA攻击，但真正实践时，效率实在低下，总结一下我们的目标：

  1. 差分故障分析，传入正确密文和一系列故障密文，就直接返回第十轮的轮密钥甚至是主密钥
  2. 基于AES的轮密钥恢复主密钥

基于以上需求，推荐两个开源项目：Stark 与 phoenixAES，stark用于基于轮密钥获取主密钥，支持DES、AES、SM4等算法，具体原理可自行查阅源码。phoenixAES能够根据传入的正确密文和一系列故障密文，返回第十轮的轮密钥甚至是主密钥，并且支持加密与解密。

phoenixAES 可以通过pip直接安装，tracefile中，第一行传正确密文，后面传入故障密文。

1
2
3
4
5
6
7
8
9
import phoenixAES
 
with open('tracefile', 'wb') as t:
    t.write("""77432fc75482b8f07009389f2ce7c8f4
90432fc75482b82d70093b9f2c3cc8f4
0b432fc75482b8547009339f2c6bc8f4
     """.encode('utf8'))
 
phoenixAES.crack_file('tracefile', [], True, False, 3)

phoenixAES很好用，有以下优点：

  1. 具备良好的输出日志，比如上面的情况中只提供了两组故障密文，无法还原出完整的轮密钥，那么它会打印出已还原的部分，未还原的部分用星号表示。

  1. 会检测输入的故障密文是否合规，可用就用，不可用就放弃此密文。
    如果错误密文为四字节，且是四种模式之一，那么我们知道这是一个正确时机的故障，工具会输出 good candidate。
    如果时机晚，错误密文少于四字节，工具会提示 too few impact。
    时机早，错误密文超过四字节，会提示 too much impact。

  2. 它支持加密和解密，本文只讲了加密，解密其实技术上也类似。crack_file函数的第三个参数传False即代表解密。在解密情况中，首行放正确明文，后面是故障明文。

二、 实现故障&捕获故障密文

我们学习了DFA的原理，以及其实现工具phoenixAES。那么问题来了，我们用什么工具实现故障，以及捕获故障密文。

2-1 源码

如果我们直接获取到了源码，那当然是最好的，在程序中修改一个字节以及打印结果可以说毫无压力。虽然现实场景中不太可能获取到源码，但是把白盒程序按执行流抠出来，用某种高级语言复写，比如C/Python，那和源码没两样。

有的朋友可能会困惑，既然都抠出代码了，为什么还要还原Key，直接跑不也挺好？在有白盒程序源码的情况下，并不特别需要还原出Key，我们可以用这个场景来练习对DFA的掌握程度。

2-2 IDA

使用IDA动态调试配合IDAPython脚本，可以很好的完成需求，但许多样本都会检测和对抗IDA动态调试，因此不是一个特别好的方案。本系列文章不会展开讨论这个方案。

2-3 Frida

Frida 可以很轻松的实现多次执行目标函数、修改 state 一个字节，打印输出等步骤，是最好的办法之一。

2-4 Unidbg

Unidbg 和 Frida 一样，都是非常好的方案，也是系列文章介绍的重点。

三、 使用源码进行DFA攻击

接下来我们讨论有源码情况下，对白盒化AES的DFA攻击怎么实现。

示例一

如下代码从变量命名上可以看出，像是IDA F5的伪代码，被作者抠出来用Python复写出来的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
import ctypes
 
dword_6661C0 = []
byte_6651C0 = []
with open("tables/6661C0.txt", "r")as F:
    dword_6661C0 = eval(F.read().strip())
    F.close()
 
with open("tables/6651C0.txt", "r")as F:
    byte_6651C0 = eval(F.read().strip())
    F.close()
 
 
byte_6650C0 = [0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,1,0,3,2,5,4,7,6,9,8,11,10,13,12,15,14,2,3,0,1,6,7,4,5,10,11,8,9,14,15,12,13,3,2,1,0,7,6,5,4,11,10,9,8,15,14,13,12,4,5,6,7,0,1,2,3,12,13,14,15,8,9,10,11,5,4,7,6,1,0,3,2,13,12,15,14,9,8,11,10,6,7,4,5,2,3,0,1,14,15,12,13,10,11,8,9,7,6,5,4,3,2,1,0,15,14,13,12,11,10,9,8,8,9,10,11,12,13,14,15,0,1,2,3,4,5,6,7,9,8,11,10,13,12,15,14,1,0,3,2,5,4,7,6,10,11,8,9,14,15,12,13,2,3,0,1,6,7,4,5,11,10,9,8,15,14,13,12,3,2,1,0,7,6,5,4,12,13,14,15,8,9,10,11,4,5,6,7,0,1,2,3,13,12,15,14,9,8,11,10,5,4,7,6,1,0,3,2,14,15,12,13,10,11,8,9,6,7,4,5,2,3,0,1,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1,0]
 
 
 
for i in range(len(dword_6661C0)):
    dword_6661C0[i]=ctypes.c_uint32(dword_6661C0[i]).value
 
for i in range(len(byte_6651C0)):
    byte_6651C0[i]=ctypes.c_uint8(byte_6651C0[i]).value
 
 
def swap(s):
    res = [i for i in range(16)]
    res[0] = s[0]
    res[1] = s[5]
    res[2] = s[10]
    res[3] = s[15]
    res[4] = s[4]
    res[5] = s[9]
    res[6] = s[0xe]
    res[7] = s[3]
    res[8] = s[8]
    res[9] = s[0xd]
    res[10] = s[2]
    res[11] = s[7]
    res[12] = s[0xc]
    res[13] = s[1]
    res[14] = s[6]
    res[15] = s[0xb]
    return "".join(res)
 
 
def xor(a,b):
    return "".join(chr(ord(a[i])^ord(b[i])) for i in range(16))
 
 
def encrypt(inp):
    for v8 in range(9):
        res = [i for i in range(16)]
        inp = swap(inp)
        for v9 in range(4):
            v3 = dword_6661C0[((4 * v9 + 16 * v8) << 8) + ord(inp[4*v9])]
            v4 = dword_6661C0[((4 * v9 + 1 + 16 * v8) << 8) + ord(inp[4*v9+1])]
            v5 = dword_6661C0[((4 * v9 + 2 + 16 * v8) << 8) + ord(inp[4*v9+2])]
            v6 = dword_6661C0[((4 * v9 + 3 + 16 * v8) << 8) + ord(inp[4*v9+3])]
            res[4*v9] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])]  | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
            v3 = v3 >> 8
            v4 = v4 >> 8
            v5 = v5 >> 8
            v6 = v6 >> 8
            res[4*v9+1] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
            v3 = v3 >> 8
            v4 = v4 >> 8
            v5 = v5 >> 8
            v6 = v6 >> 8
            res[4*v9+2] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
            v3 = v3 >> 8
            v4 = v4 >> 8
            v5 = v5 >> 8
            v6 = v6 >> 8
            res[4*v9+3] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
        inp = "".join(res)
 
    inp = swap(inp)
    res = [i for i in range(16)]
 
    for i in range(16):
        res[i] = "{:02x}".format(byte_6651C0[256*i + ord(inp[i])])
    inp = "".join(res)
    return inp
 
print(encrypt("0123456789abcdef"))

在上一篇文中我们提到，在对标准AES实现做DFA时，需要找到合适的位置修改 state 中一个字节，贴一下之前的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def encrypt(input_bytes, kList):
    '''
 
    :param input_bytes: 输入的明文
    :param kList: K0-K10
    :return:
    '''
    plainState = text2matrix(input_bytes)
    # 初始轮密钥加
    state = AddRoundKeys(plainState, kList[0:4])
    for i in range(1, 10):
        state = SubBytes(state)
        state = ShiftRows(state)
        # 第九轮列混淆前将state第一个字节改为3
        if(i==9):
            state[0][0] = 3
        state = MixColumns(state)
        state = AddRoundKeys(state, kList[4 * i:4 * (i + 1)])
 
    state = SubBytes(state)
    state = ShiftRows(state)
    state = AddRoundKeys(state, kList[40:44])
    return state

那么在白盒化的AES实现中，可以找到对应的第九轮，对应的那个时机，对应的state吗？这就是DFA 运用于白盒之上的三个重要问题。

仔细观察swap函数，它其实就是ShiftRows步骤，而除此之外的其余步骤，找不到踪迹，即其余三个步骤被整合后以查表方式实现功能。

除此之外，我们没法依赖标准实现中轮运算里步骤的先后顺序来推断白盒实现，因为在密码白盒化过程中，这些步骤的顺序可能被打破重组。

但不要慌，我们对三个问题逐个讨论，首先是“轮"的概念。我们发现，swap函数调用了十次，前九次是较复杂的查表运算:

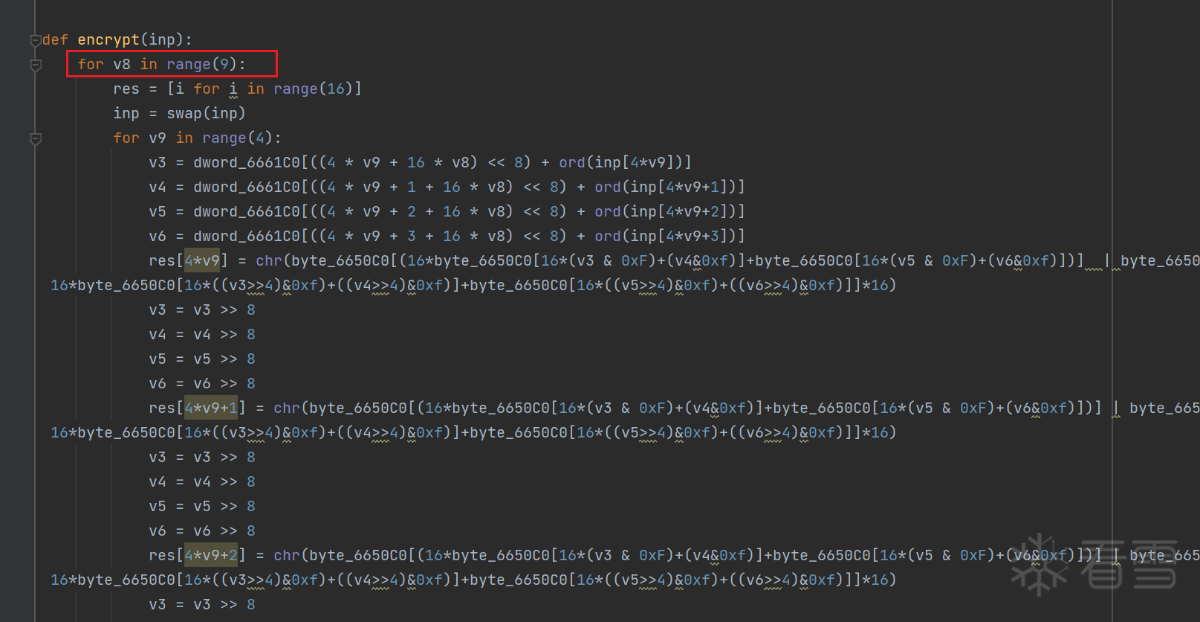
最后一轮是较为简单的查表:

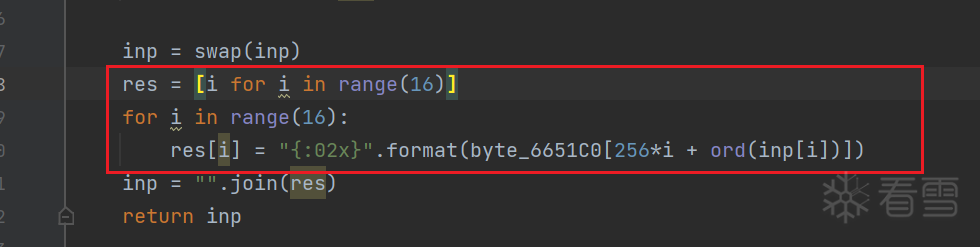
对照一下标准AES实现——最后一轮少了最为复杂的列混淆步骤。

两相对比后意识到，我们遇到的这个AES白盒实现，它和标准AES之间像是有一种微妙的联系和对应。即标准的十轮和白盒化的十轮是隐约对应的，这就实现了”轮“上的对应。

接下来考虑修改的时机，在前文我们验证过，倒数两次列混淆之间都是等价且适宜的时机。在标准AES实现中，因为第十轮不存在列混淆步骤，所以”倒数两次列混淆之间“就指的是第八轮以及第九轮运算中两次列混淆之间的时机。进而我们可以说，”第九轮运算起始处“这个时机点一定是合适的，因为它处于整个时机的中间部分。

回到样本这个白盒加密，我们说它和标准AES之间像是有一种微妙的联系和对应，那么，在它的第九轮起始处做故障注入，是否会是一个好的时机呢？我们先这么假定。

轮和时机都找到了，接下来找 state 。

我们发现，inp变量疑似 state。怎么做出的这个判断？前文我们说过，数据以state的形式计算、中间存储和传输，也可以反过来说，负责计算、中间存储和传输功能的那个变量就是 state。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
for v8 in range(9):
    res = [i for i in range(16)]
    inp = swap(inp)
    for v9 in range(4):
        v3 = dword_6661C0[((4 * v9 + 16 * v8) << 8) + ord(inp[4*v9])]
        v4 = dword_6661C0[((4 * v9 + 1 + 16 * v8) << 8) + ord(inp[4*v9+1])]
        v5 = dword_6661C0[((4 * v9 + 2 + 16 * v8) << 8) + ord(inp[4*v9+2])]
        v6 = dword_6661C0[((4 * v9 + 3 + 16 * v8) << 8) + ord(inp[4*v9+3])]
        res[4*v9] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])]  | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
        v3 = v3 >> 8
        v4 = v4 >> 8
        v5 = v5 >> 8
        v6 = v6 >> 8
        res[4*v9+1] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
        v3 = v3 >> 8
        v4 = v4 >> 8
        v5 = v5 >> 8
        v6 = v6 >> 8
        res[4*v9+2] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
        v3 = v3 >> 8
        v4 = v4 >> 8
        v5 = v5 >> 8
        v6 = v6 >> 8
        res[4*v9+3] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
    inp = "".join(res)

res 运算的结果最后赋值给inp，inp参与下一轮运算，并接收下一轮的结果循环往复，我们猜测 inp 就是state。而且从形式上看，inp在程序中是十六字节形式，这也和 state 所需一致。

下面尝试注入故障，并根据密文结果来验证我们的猜测是否正确。首先记录正常运行的结果:

e2cea35825826c8c5d3e7d6cea9d98f1，在第九轮起始处修改inp的一个字节。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def encrypt(inp):
    for v8 in range(9):
        if v8 == 8:
            # 修改第一个字节
            inpList = list(inp)
            inpList[0] = "0"
            inp = "".join(inpList)
             
        res = [i for i in range(16)]
        inp = swap(inp)
        for v9 in range(4):
            v3 = dword_6661C0[((4 * v9 + 16 * v8) << 8) + ord(inp[4*v9])]
            v4 = dword_6661C0[((4 * v9 + 1 + 16 * v8) << 8) + ord(inp[4*v9+1])]
            v5 = dword_6661C0[((4 * v9 + 2 + 16 * v8) << 8) + ord(inp[4*v9+2])]
            v6 = dword_6661C0[((4 * v9 + 3 + 16 * v8) << 8) + ord(inp[4*v9+3])]
            res[4*v9] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])]  | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
            v3 = v3 >> 8
            v4 = v4 >> 8
            v5 = v5 >> 8
            v6 = v6 >> 8
            res[4*v9+1] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
            v3 = v3 >> 8
            v4 = v4 >> 8
            v5 = v5 >> 8
            v6 = v6 >> 8
            res[4*v9+2] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
            v3 = v3 >> 8
            v4 = v4 >> 8
            v5 = v5 >> 8
            v6 = v6 >> 8
            res[4*v9+3] = chr(byte_6650C0[(16*byte_6650C0[16*(v3 & 0xF)+(v4&0xf)]+byte_6650C0[16*(v5 & 0xF)+(v6&0xf)])] | byte_6650C0[16*byte_6650C0[16*((v3>>4)&0xf)+((v4>>4)&0xf)]+byte_6650C0[16*((v5>>4)&0xf)+((v6>>4)&0xf)]]*16)
        inp = "".join(res)
 
    inp = swap(inp)
    res = [i for i in range(16)]
    for i in range(16):
        res[i] = "{:02x}".format(byte_6651C0[256*i + ord(inp[i])])
    inp = "".join(res)
    return inp

运行结果：44cea35825826c0c5d3e556cea3798f1

两相对比

1
2
e2 ce a3 58 25 82 6c 8c 5d 3e 7d 6c ea 9d 98 f1
44 ce a3 58 25 82 6c 0c 5d 3e 55 6c ea 37 98 f1

我们发现第一、第八、第十一、第十四字节和正确密文不同，完美符合DFA成功注入的特征。

接下来变化注入故障的位置以及故障值，inpList[index] = x，修改index以及x。收集故障密文，放入phoenixAES。别忘了，第一行是正确密文，之后是故障密文。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import phoenixAES
 
 
with open('tracefile', 'wb') as t:
    t.write("""e2cea35825826c8c5d3e7d6cea9d98f1
44cea35825826c0c5d3e556cea3798f1
a9cea35825826c9c5d3e546cea4698f1
e2cea39c2582c38c5d127d6c129d98f1
e2cea3c525821c8c5d7f7d6c4a9d98f1
e2ce845825e56c8c903e7d6cea9d98cc
e2ce345825cb6c8c5e3e7d6cea9d9855
e214a358de826c8c5d3e7deeea9d2ef1
e262a35846826c8c5d3e7df4ea9d99f1
     """.encode('utf8'))
 
phoenixAES.crack_file('tracefile', [], True, False, 3)

顺利运行出结果

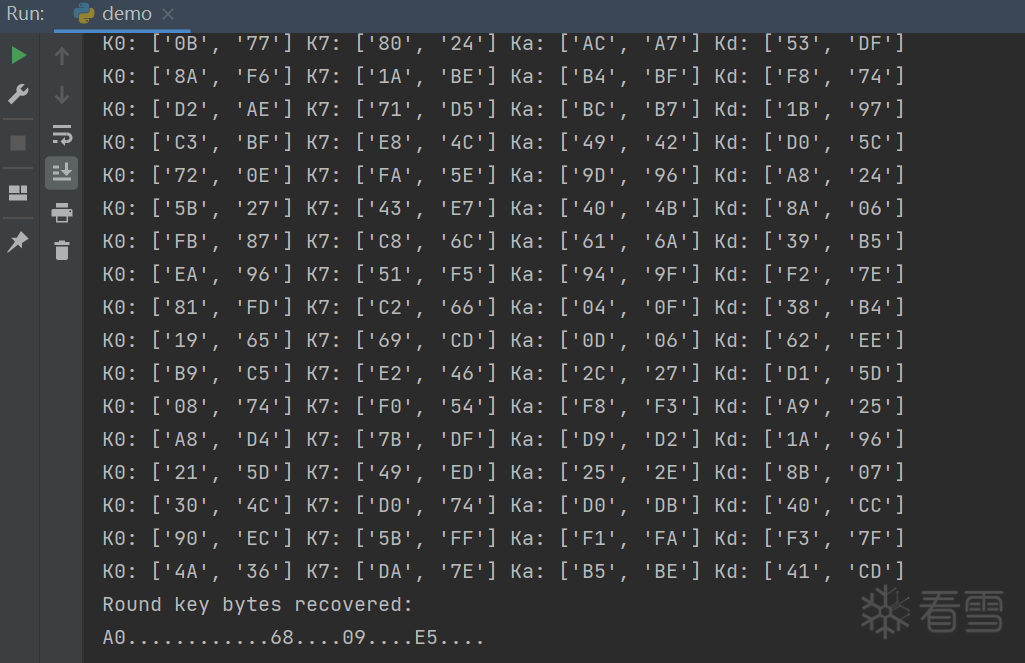
1
2
Round key bytes recovered:
4E44EACD3F54F5B54A4FB15E0710B974

如果读者仍未完全出结果，就多塞几个故障密文。

最后用 stark 求出主密钥 61316C5F7434623133355F525F6F5235

1
2
3
4
5
6
7
8
9
10
11
12
C:\Users\xxx\CLionProjects\mystark\cmake-build-debug>mystark.exe 4E44EACD3F54F5B54A4FB15E0710B974 10
K00: 61316C5F7434623133355F525F6F5235
K01: C831FA90BC0598A18F30C7F3D05F95C6
K02: 051B4EE0B91ED641362E11B2E6718474
K03: A244DC6E1B5A0A2F2D741B9DCB059FE9
K04: C19FC271DAC5C85EF7B1D3C33CB44C2A
K05: 5CB6279A8673EFC471C23C074D76702D
K06: 44E7FF79C29410BDB3562CBAFE205C97
K07: B3AD77C27139677FC26F4BC53C4F1752
K08: B75D7729C6641056040B5B9338444CC1
K09: B7740F2E71101F78751B44EB4D5F082A
K10: 4E44EACD3F54F5B54A4FB15E0710B974

我们在自己的Aes-128Encrypt中验证一番:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
Sbox = (
    0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
    0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
    0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
    0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
    0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
    0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
    0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
    0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
    0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
    0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
    0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
    0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
    0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
    0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
    0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
    0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
 
Rcon = (0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36)
 
 
def text2matrix(text):
    matrix = []
    for i in range(16):
        byte = (text >> (8 * (15 - i))) & 0xFF
        if i % 4 == 0:
            matrix.append([byte])
        else:
            matrix[i // 4].append(byte)
    return matrix
 
 
def shiftRound(array, num):
    '''
 
    :param array: 需要循环左移的数组
    :param num: 循环左移的位数
    :return: 使用Python切片，返回循环左移num个单位的array
    '''
    return array[num:] + array[:num]
 
 
def g(array, index):
    '''
    g 函数
    :param array: 待处理的四字节数组
    :index:从1-10，每次使用Rcon中不同的数
    '''
    # 首先循环左移1位
    array = shiftRound(array, 1)
    # 字节替换
    array = [Sbox[i] for i in array]
    # 首字节和rcon中对应元素异或
    array = [(Rcon[index] ^ array[0])] + array[1:]
    return array
 
 
def xorTwoArray(array1, array2):
    '''
    返回两个数组逐元素异或的新数组
    :param array1: 一个array
    :param array2: 另一个array
    :return:
    '''
    assert len(array1) == len(array2)
    return [array1[i] ^ array2[i] for i in range(len(array1))]
 
 
def showRoundKeys(round_keys):
    # 将轮密钥从44*4转成11*16
    kList = [[] for i in range(11)]
    for i in range(len(round_keys)):
        kList[i // 4] += round_keys[i]
    for i in range(len(kList)):
        print("K%02d:" % i + "".join("%02x" % k for k in kList[i]))
 
 
def keyExpand(key):
    master_key = text2matrix(key)
    round_keys = [[0] * 4 for i in range(44)]
    # 规则一(图中红色部分)
    for i in range(4):
        round_keys[i] = master_key[i]
    for i in range(4, 4 * 11):
        # 规则二(图中红色部分)
        if i % 4 == 0:
            round_keys[i] = xorTwoArray(g(round_keys[i - 1], i // 4), round_keys[i - 4])
        # 规则三(图中橙色部分)
        else:
            round_keys[i] = xorTwoArray(round_keys[i - 1], round_keys[i - 4])
    showRoundKeys(round_keys)
    return round_keys
 
 
def AddRoundKeys(state, roundKey):
    result = [[] for i in range(4)]
    for i in range(4):
        result[i] = xorTwoArray(state[i], roundKey[i])
 
    return result
 
 
def SubBytes(state):
    result = [[] for i in range(4)]
    for i in range(4):
        result[i] = [Sbox[i] for i in state[i]]
    return result
 
 
def ShiftRows(s):
    s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
    s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
    s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]
    return s
 
 
def mul_by_02(num):
    if num < 0x80:
        res = (num << 1)
    else:
        res = (num << 1) ^ 0x1b
    return res % 0x100
 
 
def mul_by_03(num):
    return mul_by_02(num) ^ num
 
 
def MixColumns(state):
    for i in range(4):
        s0 = mul_by_02(state[i][0]) ^ mul_by_03(state[i][1]) ^ state[i][2] ^ state[i][3]
        s1 = state[i][0] ^ mul_by_02(state[i][1]) ^ mul_by_03(state[i][2]) ^ state[i][3]
        s2 = state[i][0] ^ state[i][1] ^ mul_by_02(state[i][2]) ^ mul_by_03(state[i][3])
        s3 = mul_by_03(state[i][0]) ^ state[i][1] ^ state[i][2] ^ mul_by_02(state[i][3])
        state[i][0] = s0
        state[i][1] = s1
        state[i][2] = s2
        state[i][3] = s3
 
    return state
 
 
def state2Text(state):
    text = sum(state, [])
    return "".join("%02x" % k for k in text)
 
 
def encrypt(input_bytes, kList):
    '''
 
    :param input_bytes: 输入的明文
    :param kList: K0-K10
    :return:
    '''
    plainState = text2matrix(input_bytes)
    # 初始轮密钥加
    state = AddRoundKeys(plainState, kList[0:4])
    for i in range(1, 10):
        state = SubBytes(state)
        state = ShiftRows(state)
        state = MixColumns(state)
        state = AddRoundKeys(state, kList[4 * i:4 * (i + 1)])
 
    state = SubBytes(state)
    state = ShiftRows(state)
    state = AddRoundKeys(state, kList[40:44])
    return state
 
 
# 0123456789abcdef
input_bytes = 0x30313233343536373839616263646566
key = 0x61316C5F7434623133355F525F6F5235
kList = keyExpand(key)
cipherState = encrypt(input_bytes, kList)
cipher = state2Text(cipherState)
print(cipher)

可以发现结果完全正确。

示例二

这是 网上冲浪 时在博主文章里看到的一个例子。在这个白盒实现中，同样存在数个大表，我们将其放在头文件里。而且从函数名可知，这是一个白盒解密函数。解密和加密在处理上有细微不同，借这个例子好好讨论一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
#include "tables.h"
 
// extern "C" _declspec(dllexport) int WBACRAES_DecryptOneBlock(unsigned __int8 *a2, unsigned __int8 *a3, int a4);
 
int WBACRAES_DecryptOneBlock(unsigned __int8 *a2, unsigned __int8 *a3, int a4)
{
    unsigned __int8 (*v5)[8]; // r3
    int v6; // r11
    char *v7; // r1
    int v8; // r3
    _DWORD *v9; // r6
    int j; // r2
    int v11; // r10
    int v12; // r0
    int v13; // r0
    void **v14; // r8
    int v15; // r0
    int k; // r2
    char *v17; // r3
    char v18; // r5
    int v19; // r0
    char v20; // r1
    int v21; // r6
    unsigned int v22; // r5
    int v23; // r1
    char v24; // r8
    _BYTE *v25; // r12
    int v26; // r12
    int v27; // r7
    _BYTE *v28; // r8
    int v29; // r8
    int v30; // r7
    int v31; // r2
    char *v32; // r1
    int i; // r3
    _BYTE *v34; // r5
    int v35; // r8
    char *v36; // r6
    int v37; // r8
    int l; // r3
    int m; // r2
    int v41; // [sp+0h] [bp-E0h]
    _BYTE *v42; // [sp+4h] [bp-DCh]
    int v43; // [sp+8h] [bp-D8h]
    int v44; // [sp+Ch] [bp-D4h]
    int v47; // [sp+1Ch] [bp-C4h]
    char v49[4]; // [sp+30h] [bp-B0h] BYREF
    int v50; // [sp+34h] [bp-ACh]
    _DWORD s[42]; // [sp+38h] [bp-A8h] BYREF
 
    memset(s, 0, 0x20u);
    for (int i=0; i!=4; i++) {
        for(int j=0; j!=4; j++) {
            *((_BYTE *)s + i + 8 * j) = *((_BYTE *)a2 + 4 * i + j);
        }
    }
 
    v44 = 0;
    if ( !v44 )
    {
        v6 = 10;
        while ( v6 >= a4 )
        {
            if ( !--v6 )
            {
                if ( a4 == 1 )
                {
                    s[8] = s[0];
                    s[9] = s[1];
                    s[10] = s[2];
                    s[11] = s[3];
                    s[12] = s[4];
                    s[13] = s[5];
                    s[14] = s[6];
                    s[15] = s[7];
                    v30 = 1;
                    do
                    {
                        v31 = 0;
                        v32 = (char *)&unk_18D8E;
                        for ( i = 0; i != 4; ++i )
                        {
                            v34 = invFirstRoundTable_auth1;
                            v35 = (v32[1] + (_BYTE)v6) & 3;
                            v32 += 2;
                            v36 = (char *)&s[2 * i + 32] + v35;
                            v37 = i + 4 * v35;
                            *((_BYTE *)s + v6 + v31) = *((_BYTE *)v34 + 256 * v37 + (unsigned __int8)*(v36 - 96));
                            v31 += 8;
                        }
                        ++v6;
                    }
                    while ( v6 != 4 );
                }
                break;
            }
 
            v7 = (char *)&unk_18D8E;
            v8 = 0;
            v47 = 4 * v6;
            do
            {
                v9 = &s[2 * v8 + 32];
                for ( j = 0; j != 4; ++j )
                {
                    v11 = 1;
                    v15 = (v7[1] + (_BYTE)j) & 3;
                    v50 = invRoundTables_auth1[256 * (v8 + 4 * (v15 + v47)) + *((unsigned __int8 *)v9 + v15 - 128)];
                    s[4 * v8 + 16 + j] = v50;
                }
                ++v8;
                v7 += 2;
            }
            while ( v8 != 4 );
 
 
            for ( k = 0; k != 4; ++k )
            {
                v17 = (char *)&s[16] + k;
                v41 = 0;
                do
                {
                    v43 = 0;
                    v49[1] = v17[16];
                    v18 = *v17;
                    v19 = 96 * v6 + 24 * v41;
                    v49[2] = v17[32];
                    v20 = v17[48];
                    v21 = v18 & 0xF;
                    v49[0] = v18;
                    v22 = v18 & 0xF0;
                    v49[3] = v20;
                    v23 = 6 * k;
                    do
                    {
                        v24 = v49[++v43];
                        v25 = invXorTables_auth1;
                        v42 = v25;
                        v26 = v23 + 1;
                        v27 = v24 & 0xF0 | (v22 >> 4);
                        LOBYTE(v21) = v42[256 * (v19 + v23) + (v21 | (16 * (v24 & 0xF)))] & 0xF;
                        v28 = invXorTables_auth1;
                        v23 += 2;
                        v22 = (unsigned __int8)(16 * *((_BYTE *)v28 + 256 * (v26 + v19) + v27));
                    }
                    while ( v43 != 3 );
                    v29 = v41;
                    v17 += 4;
                    *((_BYTE *)&s[2 * k] + v41++) = v22 | v21;
                }
                while ( v29 != 3 );
            }
        }
        for ( l = 0; l != 4; ++l )
        {
            for ( m = 0; m != 4; ++m )
                a3[4 * l + m] = *((_BYTE *)&s[2 * m] + l);
        }
    }
    return v44;
}
 
int main() {
    _BYTE a2[16] = {0x8D, 0x63, 0xD7, 0x56, 0xDB, 0x55, 0xCD, 0x06, 0x56, 0x70, 0xB9, 0x74, 0xE6, 0x24, 0xB5, 0x86};
    _BYTE a3[16];
    int ret;
    for(int i=0; i<16; i++){
        printf("%02X ", a2[i]);
    }
    printf("\n");
    ret = WBACRAES_DecryptOneBlock(a2, a3, 1);
 
    for(int i=0; i<16; i++){
        printf("%02X", a3[i]);
    }
    printf("\n");
 
    return 0;
}

如法炮制，首先寻找“轮”：

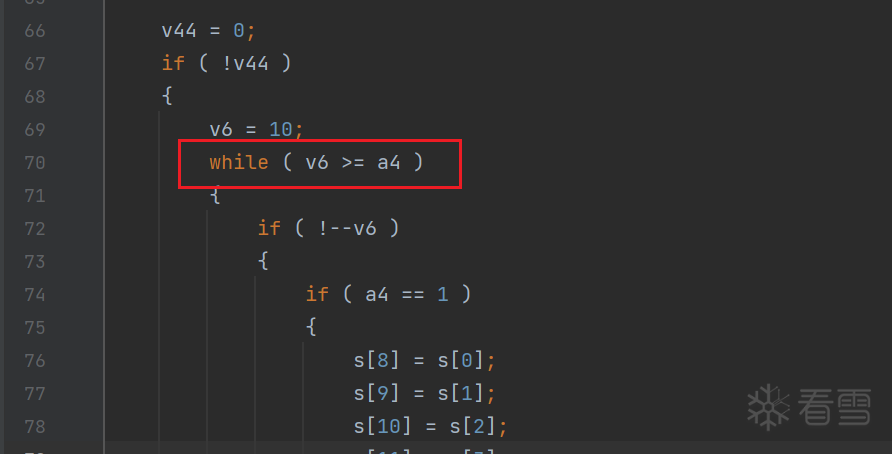
我们发现主函数内部有一个大的循环，但单纯静态看，看不太出有几轮，我添加了计数器，打印输出一下。

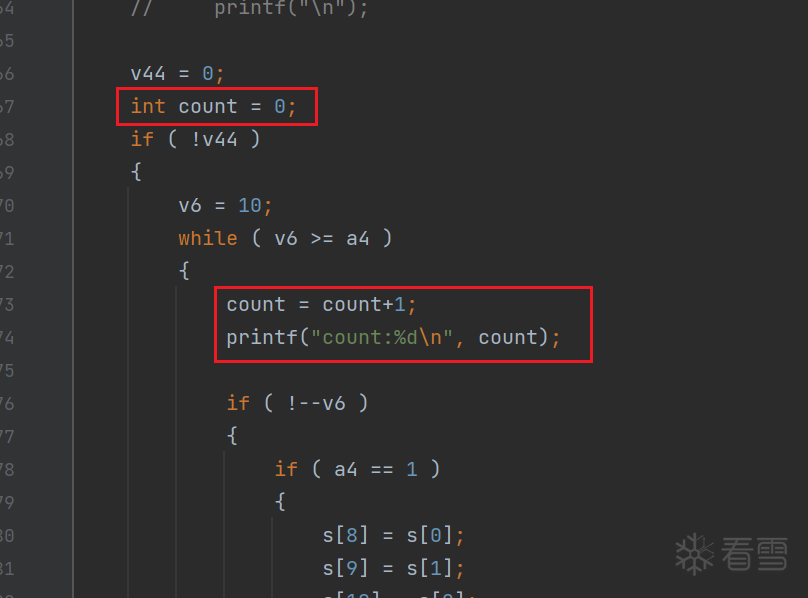
运行效果如下：

1
2
3
4
5
6
7
8
9
10
11
12
8D 63 D7 56 DB 55 CD 06 56 70 B9 74 E6 24 B5 86
count:1
count:2
count:3
count:4
count:5
count:6
count:7
count:8
count:9
count:10
759E385FF20421ECE9118FEFC7D9BF6D

可以发现，在整个解密过程中，存在十轮运算。这和上个例子类似，让我们看到了希望。需要注意，有一些更好的白盒实现中，找不到明显的“轮”，或者并非9/10次循环，那就麻烦了。

找到轮之后，我们将时机确定在第九轮开始处，接下来找 state 。我认为变量 s 比较像存放state的变量，或者说，它像一个结构体，其中一部分是 state。

这是我们的输入密文：8D 63 D7 56 DB 55 CD 06 56 70 B9 74 E6 24 B5 86，它被放在了s中。

1
2
3
4
5
for (int i=0; i!=4; i++) {
    for(int j=0; j!=4; j++) {
        *((_BYTE *)s + i + 8 * j) = *((_BYTE *)a2 + 4 * i + j);
    }
}

除此之外，s在程序中大量参与运算。比较符合 state 计算、中间存储和传输的功能需求。如果我们判断错误，那也问题不大，大不了重新猜嘛。

我们并不会像例一那样，修改s指向的前十六个字节块，因为我们观察到，输入密文被放到了内存中第1-4、9-12、17-20、25-28这四块偏移里。

1
2
8d db 56 e6   00 00 00 00   63 55 70 24   00 00 00 00   │ ··V·····cUp$···· │
d7 cd b9 b5   00 00 00 00   56 06 74 86   00 00 00 00   │ ········V·t····· │

debug查看第九轮起始处 s 的情况：

1
2
53 eb 73 a2   00 00 00 00   ba 37 b0 e4   00 00 00 00   │ S·s······7······ │
bf 16 ab 7c   00 00 00 00   f9 a6 b0 a7   00 00 00 00   │ ···|············ │

int 在内存里是小端序，所以注入故障，将0xa273eb53 修改成 0xa273eb52，修改了最低的一字节。

1
2
3
4
5
if(count==9){
    //  53 eb 73 a2   00 00 00 00   ba 37 b0 e4   00 00 00 00   │ S·s······7······ │
    //  bf 16 ab 7c   00 00 00 00   f9 a6 b0 a7   00 00 00 00   │ ···
    s[0] = 0xa273eb52;
}

运行查看结果，解密时和加密同理，会有四个字节发生改变，但所改变的四个字节和加密过程中不同，不必死记硬背，直接把正确输出输出和故障输出放入 phoenixAES，crack_file的第三个参数传入False，代表这是一个解密过程。

1
2
3
4
5
6
7
8
9
import phoenixAES
 
 
with open('tracefile', 'wb') as t:
    t.write("""759E385FF20421ECE9118FEFC7D9BF6D
A39E385FF2D521ECE91183EFC7D9BF96
     """.encode('utf8'))
 
phoenixAES.crack_file('tracefile', [], False, False, 3)

运行

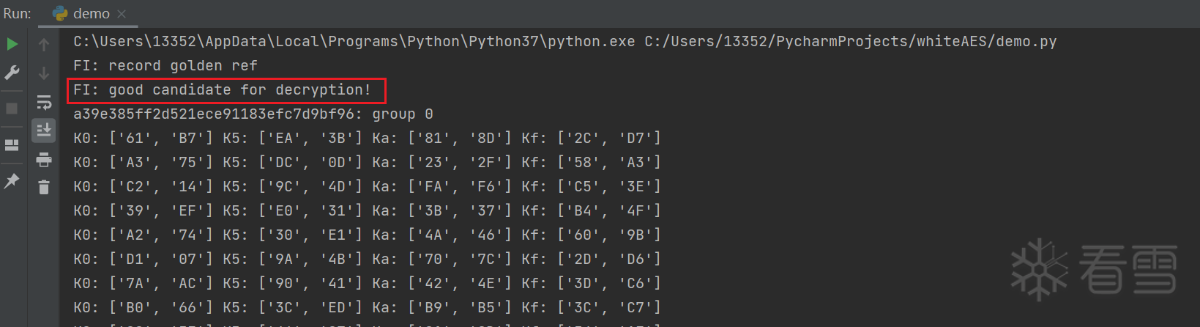
可以发现，日志非常清晰的告诉我们，这是一个合格的故障明文，适合解密场景。而且下一样还说，它属于”group 0“，即四种模式中的第一种。

为什么 phoenixAES 能做到？因为在它内部保存了对应关系

1
2
3
4
5
6
7
8
9
10
11
12
AesFaultMaps= [
# AES decryption
 [[True, False, False, False, False, True, False, False, False, False, True, False, False, False, False, True],
  [False, True, False, False, False, False, True, False, False, False, False, True, True, False, False, False],
  [False, False, True, False, False, False, False, True, True, False, False, False, False, True, False, False],
  [False, False, False, True, True, False, False, False, False, True, False, False, False, False, True, False]],
# AES encryption
 [[True, False, False, False, False, False, False, True, False, False, True, False, False, True, False, False],
  [False, True, False, False, True, False, False, False, False, False, False, True, False, False, True, False],
  [False, False, True, False, False, True, False, False, True, False, False, False, False, False, False, True],
  [False, False, False, True, False, False, True, False, False, True, False, False, True, False, False, False]]
]

这给我们带来了两点启发

  • 如果记不住加密以及解密到底有哪几种故障模式，甚至记不住到底影响了几个字节，那就把正确输入和故障输入塞给phoenixAES，让它来判断，但一定要根据加解密模式传入正确的第三个参数给crack_file API。
  • 如果没法判断一个程序是白盒化加密还是白盒化解密，可以通过故障输出属于加密还是解密的故障模式来判断。

接下来多次修改state，记录输出的故障明文

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 第一次修改，s的第一个字节
s[0] = 0xa273eb52;
// 第二次修改，s的第一个字节
s[0] = 0xa273eb51;
// 第三次修改，s的第二个字节
s[0] = 0xa273ec53;
// 第四次修改，s的第二个字节
s[0] = 0xa273ed53;
// 第五次修改，s的第三个字节
s[0] = 0xa274eb53;
// 第六次修改，s的第三个字节
s[0] = 0xa275eb53;
// 第七次修改，s的第四个字节
s[0] = 0xa373eb53;
// 第八次修改，s的第四个字节
s[0] = 0xa473eb53;

记录的结果喂给phoenixAES

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import phoenixAES
with open('tracefile', 'wb') as t:
    t.write("""759E385FF20421ECE9118FEFC7D9BF6D
A39E385FF2D521ECE91183EFC7D9BF96
379E385FF24A21ECE91189EFC7D9BFCC
759E38AD0C0421ECE9918FEFC7D9ED6D
759E3866F90421ECE9308FEFC7D9076D
759E835FF204219904118FEFC799BF6D
759EB25FF204212240118FEFC7BBBF6D
7574385FF20425ECE9118F9EE0D9BF6D
75C4385FF20471ECE9118F6081D9BF6D
     """.encode('utf8'))
 
phoenixAES.crack_file('tracefile', [], False, False, 3)

运行

1
2
Round key bytes recovered:
F6F472F595B511EA9237685B35A8F866

在DFA作用于解密函数时，直接求得初始轮密钥K_0，按照AES密钥编排规则就是密钥本身。

可以做一下验证，我们写的Aes-128Encrypt没处理解密过程，但我们可以倒着测试，验证输出的明文+求出的Key 加密后是否等于输入，结果完全符合。

示例三

第三个例子是老版本的sgmain里的一个白盒AES，来具体看一下，主函数如下：

1
2
3
4
5
6
7
8
int main() {
    std::vector<uint8_t> encryptData;
    const char* white_iv = "6zi8tey4328TcUh1";
    uint8_t Text[] = {0x30,0x31,0x32,0x33,0x34,0x35,0x36,0x37,0x38,0x39,0x61,0x62,0x63,0x64,0x65,0x66};
    std::vector<uint8_t> data(Text, Text+16);
    encrypt(data, &encryptData, (uint8_t*)white_iv);
    return 0;
}

这个例子比前面两个难度大一些，前面的例子里，程序接收十六字节的输入，输出十六字节，即完全符合AES本身的定义。但是如果输入并非16字节呢？比如32字节或者45字节。我们需要回顾一下分组和填充的相关知识。

一种加密算法或哈希算法，潜在的、待处理的明文长度是任意且近乎无限的。有限的程序逻辑如何处理无限长的数据？这常常离不开循环。如果按照某个单位长度划分成”数块“后循环处理，这就是分组加密，所谓的某个单位长度就是分组长度。每个数据块被处理后的密文块拼接在一起，就是完整密文，如果只保留最后一个密文块，那就近似哈希算法。

分组必然存在两个问题

  • 待处理的明文并不总能被恰好分成多组
  • 不同组之间是否有关联

假设分组大小为8字节，输入如下

1
DD DD DD DD DD DD DD DD DD DD DD DD

分组后

1
| DD DD DD DD DD DD DD DD | DD DD DD DD

可以发现，第二个块不完整。因此我们需要填充——把明文填充成可以被完整分割的多个块，因为只接受固定长度的输入。填充的方案很多，每个人都能设计自己的填充方案，但有一个硬性要求——解密时，得能区分哪部分是原文，哪部分是填充。下面盘点一些填充方案

首先是补零方案

1
| DD DD DD DD DD DD DD DD | DD DD DD DD 00 00 00 00 |

在最后一个残缺块后补0到符合分组长度，这就是补零填充，解密时删掉末尾的零就行。

但如果明文如下呢？

1
DD DD DD DD DD DD DD DD DD DD 00 00

补零填充后就是

1
| DD DD DD DD DD DD DD DD | DD DD 00 00 00 00 00 00 |

那解密时，如何区分补上去的零和原文末尾本就有的零呢？除非约法三章，要求输入不以字节0结尾，否则就只能换个填充方案。

来看我们的新方案——补零+长度方案，假设末尾应该填充4个零字节，那么新方案就只填充3个，最后一字节存储所填充的总长度，此处就是4。

1
| DD DD DD DD DD DD DD DD | DD DD 00 00 00 00 00 04 |

这个新方案真不错，即使输入以零结尾也不影响我们区分填充和原文各自的部分。但还有一个隐患，如果明文恰好可以被完整分成数个组呢？这种情况下如何处理？

首先我们得问，能不补吗？能不补当然不补，大家都知道，方案越简单，漏洞越少。下面举个例子，看不补行不行。

明文A

1
DD DD DD DD DD DD DD DD DD DD DD DD DD DD 00 02

明文B

1
DD DD DD DD DD DD DD DD DD DD DD DD DD DD

明文A恰好两个分组长度，我们选择不补；明文B最后一个块缺少两字节，补完即

1
DD DD DD DD DD DD DD DD | DD DD DD DD DD DD 00 02 |

糟糕了，我们根本没办法区分这两组明文，这显然是不可接受的。因此即使输入恰好满足分组长度，也必须做填充。新规则如下：当明文恰好可以被分成多个完整的组时，就认定为缺少”一组“，明文A在这种策略下被补成

1
DD DD DD DD DD DD DD DD | DD DD DD DD DD DD 00 02 | 00 00 00 00 00 00 00 08 |

这就解决了上面模棱两可的问题，最后的方案——补零+补长度+恰好符合分组长度时补一个分组 ，这是一个完善的好方案！只可惜我们生的太晚，前人已经想到了这个方案，并将它命名为ANSI X9.23。

现行的，最通用广泛的填充标准是PKCS7，它比ANSI X9.23更优雅那么一些（填充0给人一种很敷衍的感觉）。

假设明文为

1
DD DD DD DD DD DD DD DD  |  DD DD 00 00

距离完整8字节分组少了4个字节，那么填充4个字节，且每个字节均为4。

1
DD DD DD DD DD DD DD DD  |  DD DD 00 00 04 04 04 04 |

假设明文为

1
DD DD DD DD DD DD DD DD |

那么填充 8个字节，每个字节均为 8

1
DD DD DD DD DD DD DD DD | 08 08 08 08 08 08 08 08

不管是PKCS7还是ANSI X9.23，只要分组长度不超过0xFF，都是可行的好方案，一旦分组长度超过0xFF，我们就没办法用一个字节表示长度了。除此之外，如果PKCS7的分组长度固定为8字节时，这个方案也叫PKCS5，因为AES分组长度固定为16字节，所以没法遵守PKCS5。换言之，如果对AES采用PKCS5, 那么AES也不会遵守，实质上采用PKCS7。

上面我们处理了“待处理的明文并不总能被恰好分成多组”，接下来考虑“不同组之间是否有关联”这个问题。

这是个由分组衍生出来的重要问题，叫做工作模式。首先，我们的朴素想法是，不同块之间分别加密，结果简单拼接在一起。

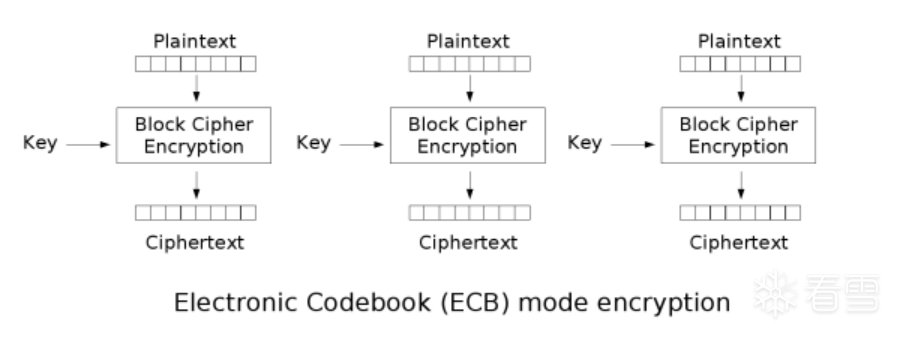
这种朴素的方案叫ECB，它有很大的优点，大量明文分组可以并行运算，并行加密。但它存在致命缺陷，由于明文块互相之间独立，所以相同的明文块会被加密成相同的密文块。那么，假设密文中有两个内容块数据一致，就可以反推对应明文内容也一致，这在某些情况下足以实施伪造和欺诈。

除此之外，业界喜欢展示ECB加密后的图片，这会清晰表现它的缺点。图片文件中，临近区块的内容往往一致，密文也一致，这使得图片轮廓清晰可见，如下是经典的企鹅加密图。

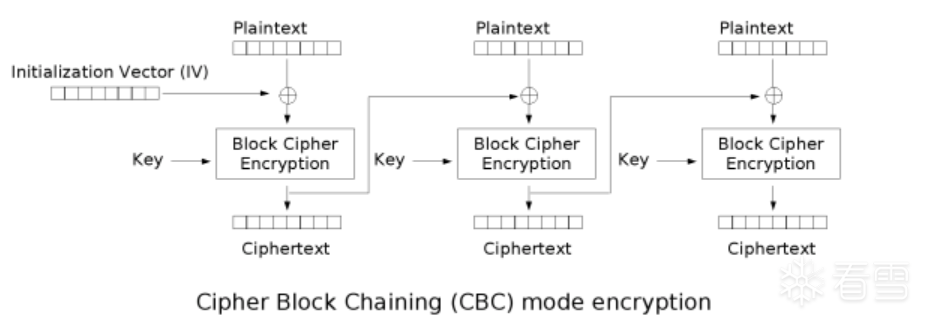
虽然有缺陷，但使用ECB的情况还是不少，因为很多开发人员并不注重安全。除了它以外，使用最多的模式是CBC。在这个模式中，每个明文块在运算前，先与前一个分组的输出结果做异或运算。因此，相同的分组内容不会带来相同输出，除非两者的前一个分组也相同。我们发现CBC中存在一个问题，最后一个输入块和前一个输出块异或，第二个输入块和第一个输出块异或，那么，第一个输入块和谁异或呢？为了处理这个问题，使用者需要传入一个和分组等长的字节串，供其异或，学名叫初始化向量，缩写IV。

整个情况如下图所示，“圈加”符号在密码学图示中出现频率很高，一般指异或运算。

除此之外还存在数种工作模式，有各种各样的优点，安全性甚至比CBC更好，但在SO中出现频率远不如ECB和CBC，这里不去提了。

温习完分组和填充的相关知识，我们回到例三。分组模式和填充会给DFA攻击带来什么影响，这是我们最关心的内容。首先，DFA攻击时，我们观察十六字节在故障注入后的密文变化，如果程序存在多个分组的输入，那多个分组的输出会影响我们收集和验证故障输出。因此我们十分希望程序的输入只有一个分组。因此我们要控制输入，在1-15个字节之间，这样填充后只会进行一个分组的加密或解密运算。（输入十六个字节时，会被填充一整组，最后导致两组加密。）

再考虑CBC模式中的IV对我们的影响。DFA不关注输入，关心的是正确输出和故障输出。在加密过程中，IV会影响验证DFA求出的密钥是否正确。在解密过程中，需要找到故障输出而非IV异或后的输出。听起来有些绕，但简而言之，为了减少IV的干扰，我建议在CBC模式中，将IV全填充为0后再做DFA。需要注意，这是指的不是字符串0，而是字节0。

如下所示，我们将IV改成全0数组，输入改成十五字节，因为样本采用PKCS7_padding，可以预料，明文末尾会填充01。不放心的可以自行debug。

1
2
3
4
5
6
7
8
9
10
int main() {
    std::vector<uint8_t> encryptData;
    //const char* white_iv = "6zi8tey4328TcUh1";
    char white_iv[16] = {0};
    //"0123456789abcde"
    uint8_t Text[] = {0x30,0x31,0x32,0x33,0x34,0x35,0x36,0x37,0x38,0x39,0x61,0x62,0x63,0x64,0x65};
    std::vector<uint8_t> data(Text, Text+15);
    encrypt(data, &encryptData, (uint8_t*)white_iv);
    return 0;
}

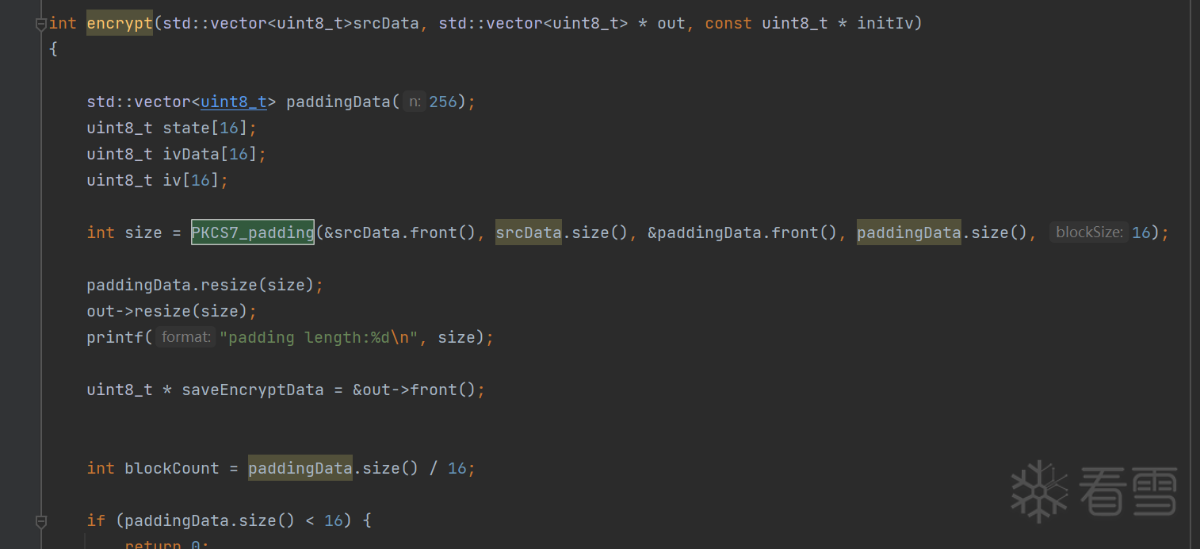
下面回归到正常的DFA流程。

首先是寻找“轮”：


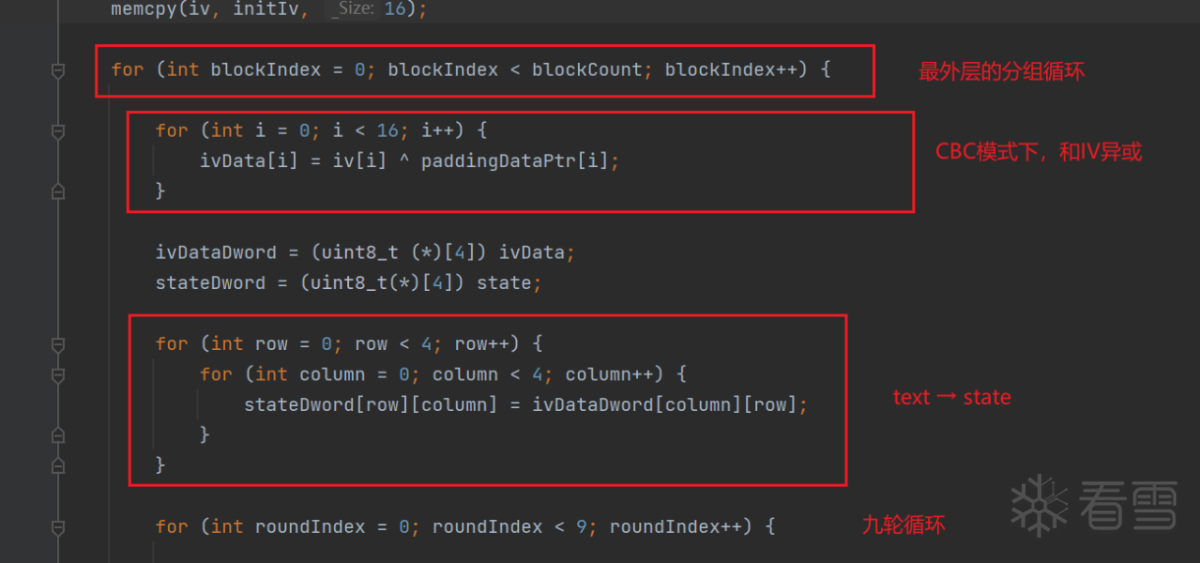
这份代码抠的很漂亮，我们发现主体是九轮运算，前面两个例子都是十轮运算，这里却少了一轮。没关系，我们还是试着在第九轮开始时做故障注入，如果效果不对，就推前到第八轮。反正可以根据结果来判断时机早了还是晚了，大不了多试几次。

代码的命名很清晰，我们不用刻意找state在哪。

首先记录正确输出

73cc1e47c49d6675de5a14273c3b046c

下面开始注入故障：

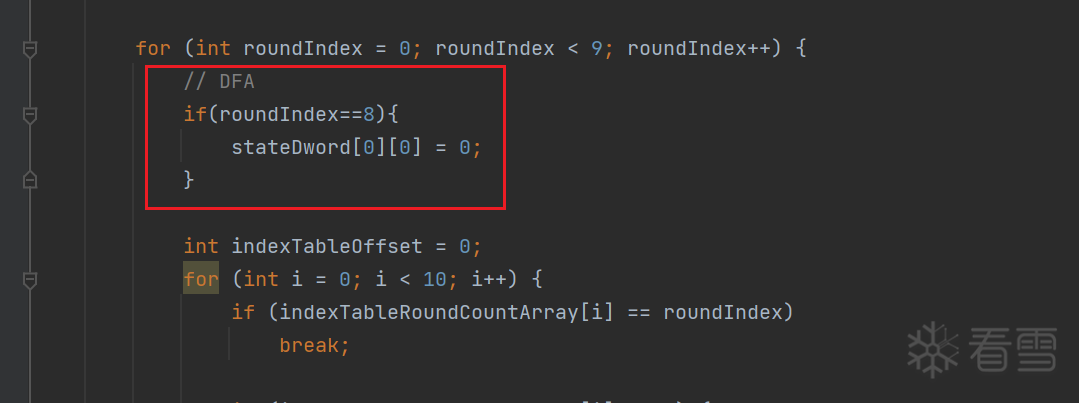
65cc1e47c49d662bde5a40273cdf046c

这个结果既熟悉又让人欣喜，这不就是加密过程中故障注入成功所呈现的四种模式中的第一种嘛。

下面继续，故障注入记录如下

1
2
3
4
5
6
7
8
stateDword[0][0] = 0;
stateDword[0][0] = 1;
stateDword[0][1] = 0;
stateDword[0][1] = 1;
stateDword[0][2] = 0;
stateDword[0][2] = 1;
stateDword[0][3] = 0;
stateDword[0][3] = 1;

将正确密文和八个故障密文丢入phoenixAES

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import phoenixAES
 
 
with open('tracefile', 'wb') as t:
    t.write("""73cc1e47c49d6675de5a14273c3b046c
65cc1e47c49d662bde5a40273cdf046c
2dcc1e47c49d66d0de5a57273cde046c
73c71e47ae9d6675de5a141e3c3b5e6c
731c1e47199d6675de5a143a3c3b476c
73ccaa47c48f6675075a14273c3b045f
73ccaf47c4706675315a14273c3b046f
73cc1e3ac49d1275de5e1427bd3b046c
73cc1e8ec49d4075deb114274c3b046c
     """.encode('utf8'))
 
phoenixAES.crack_file('tracefile', [], True, False, 3)

运行

1
2
Round key bytes recovered:
217C3F7449325ADB077F8902179858AC

放入stark

1
2
3
4
5
6
7
8
9
10
11
12
C:\Users\xxx\CLionProjects\mystark\cmake-build-debug>mystark.exe 217C3F7449325ADB077F8902179858AC 10
K00: 445352704242354C364731654E303657
K01: 4156095F03143C1335530D767B633B21
K02: B8B4F47EBBA0C86D8EF3C51BF590FE3A
K03: DC0F749867AFBCF5E95C79EE1CCC87D4
K04: 9F183C04F8B780F111EBF91F0D277ECB
K05: 43EB23D3BB5CA322AAB75A3DA79024F6
K06: 03DD618FB881C2AD12369890B5A6BC66
K07: 67B8525ADF3990F7CD0F086778A9B401
K08: 34352EE6EB0CBE112603B6765EAA0277
K09: 8342DBBE684E65AF4E4DD3D910E7D1AE
K10: 217C3F7449325ADB077F8902179858AC

即密钥 445352704242354C364731654E303657。

使用Aes-128Encrypt 验证，明文别忘了是30313233343536373839616263646501

1
2
3
4
5
6
input_bytes = 0x30313233343536373839616263646501
key = 0x445352704242354C364731654E303657
kList = keyExpand(key)
cipherState = encrypt(input_bytes, kList)
cipher = state2Text(cipherState)
print(cipher)

结果完全一致。

四、使用Unidbg进行DFA 攻击

源码进行 DFA 攻击的阶段结束，接下来，我们简单讨论使用Unidbg处理DFA。

案例的代码如下，Unidbg中有另一个办法可以帮助”找时机“。我先卖个关子，大家先往下看。

首先和前文一样，Call wbaes_encrypt_ecb。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
package com.luckin;
 
import com.github.unidbg.AndroidEmulator;
import com.github.unidbg.Module;
import com.github.unidbg.linux.android.AndroidEmulatorBuilder;
import com.github.unidbg.linux.android.AndroidResolver;
import com.github.unidbg.linux.android.dvm.AbstractJni;
import com.github.unidbg.linux.android.dvm.DalvikModule;
import com.github.unidbg.linux.android.dvm.VM;
import com.github.unidbg.memory.Memory;
import com.github.unidbg.memory.MemoryBlock;
import com.github.unidbg.pointer.UnidbgPointer;
 
import java.io.File;
 
public class LKAES extends AbstractJni {
    private final AndroidEmulator emulator;
    private final VM vm;
    private final Module module;
 
    public LKAES(){
        emulator = AndroidEmulatorBuilder.for32Bit().build(); // 创建模拟器实例，要模拟32位或者64位，在这里区分
 
        // 模拟器的内存操作接口
        final Memory memory = emulator.getMemory();
        // 设置系统类库解析
        memory.setLibraryResolver(new AndroidResolver(23));
        // 创建Android虚拟机
        vm = emulator.createDalvikVM(new File("unidbg-android/src/test/resources/luckin/ruixingkafei_4.9.3.apk"));
        vm.setVerbose(true);
        // 加载so到虚拟内存
        DalvikModule dm = vm.loadLibrary("cryptoDD", true);
        module = dm.getModule();
        // 设置JNI
        vm.setJni(this);
        dm.callJNI_OnLoad(emulator);
    }
 
    public static byte[] hexStringToBytes(String hexString) {
        if (hexString.isEmpty()) {
            return null;
        }
        hexString = hexString.toLowerCase();
        final byte[] byteArray = new byte[hexString.length() >> 1];
        int index = 0;
        for (int i = 0; i < hexString.length(); i++) {
            if (index  > hexString.length() - 1) {
                return byteArray;
            }
            byte highDit = (byte) (Character.digit(hexString.charAt(index), 16) & 0xFF);
            byte lowDit = (byte) (Character.digit(hexString.charAt(index + 1), 16) & 0xFF);
            byteArray[i] = (byte) (highDit << 4 | lowDit);
            index += 2;
        }
        return byteArray;
    }
 
    public static String bytesTohexString(byte[] bytes) {
        StringBuffer sb = new StringBuffer();
        for(int i = 0; i < bytes.length; i++) {
            String hex = Integer.toHexString(bytes[i] & 0xFF);
            if(hex.length() < 2){
                sb.append(0);
            }
            sb.append(hex);
        }
        return sb.toString();
    }
 
    public void call_wbaes(){
        MemoryBlock inblock = emulator.getMemory().malloc(16, true);
        UnidbgPointer inPtr = inblock.getPointer();
        MemoryBlock outblock = emulator.getMemory().malloc(16, true);
        UnidbgPointer outPtr = outblock.getPointer();
        byte[] stub = hexStringToBytes("30313233343536373839616263646566");
        assert stub != null;
        inPtr.write(0, stub, 0, stub.length);
        module.callFunction(emulator, 0x17bd5, inPtr, 16, outPtr, 0);
        String ret = bytesTohexString(outPtr.getByteArray(0, 0x10));
        System.out.println("white box result:"+ret);
        inblock.free();
        outblock.free();
    }
 
    public static void main(String[] args) {
        LKAES lkaes = new LKAES();
        lkaes.call_wbaes();
    }
}

运行结果：

1
2
3
4
5
6
7
8
[15:41:39 547]  INFO [com.github.unidbg.linux.AndroidElfLoader] (AndroidElfLoader:464) - libcryptoDD.so load dependency libandroid.so failed
JNIEnv->FindClass(com/luckincoffee/safeboxlib/CryptoHelper) was called from RX@0x4001b43b[libcryptoDD.so]0x1b43b
JNIEnv->RegisterNatives(com/luckincoffee/safeboxlib/CryptoHelper, RW@0x400dfd0c[libcryptoDD.so]0xdfd0c, 4) was called from RX@0x4001b3e3[libcryptoDD.so]0x1b3e3
RegisterNative(com/luckincoffee/safeboxlib/CryptoHelper, localAESWork([BI[B)[B, RX@0x4001984d[libcryptoDD.so]0x1984d)
RegisterNative(com/luckincoffee/safeboxlib/CryptoHelper, localConnectWork([B[B)[B, RX@0x4001978d[libcryptoDD.so]0x1978d)
RegisterNative(com/luckincoffee/safeboxlib/CryptoHelper, md5_crypt([BI)[B, RX@0x4001a981[libcryptoDD.so]0x1a981)
RegisterNative(com/luckincoffee/safeboxlib/CryptoHelper, localAESWork4Api([BI)[B, RX@0x4001b1cd[libcryptoDD.so]0x1b1cd)
white box result:b0f59c0d48c145915fc8f6a842c4d5eb

可以发现计算结果完全一致。

接下来我们要作图，读者可能会困惑，做什么图？事实上，因为白盒加密的主要实现方式是查表法，所以加密主体就是大量的内存访问。那么记录函数对内存的访问以及发起访问的地址（PC指针），绘制成折线图，就可以较好的反映加密流程。

使用Unidbg的ReadHook：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void traceAESRead(){
    emulator.getBackend().hook_add_new(new ReadHook() {
        @Override
        public void hook(Backend backend, long address, int size, Object user) {
            long now = emulator.getBackend().reg_read(ArmConst.UC_ARM_REG_PC).intValue();
            if((now>module.base) & (now < (module.base+module.size))){
                System.out.println(now - module.base);
            }
        }
 
        @Override
        public void onAttach(UnHook unHook) {
 
        }
 
        @Override
        public void detach() {
 
        }
    }, module.base, module.base+module.size, null);
}

规则如下：监控整个SO地址范围内的内存读取操作，记录其发起地址，我减去了SO基地址，只打印偏移，这样呈现效果更好。

traceAESRead 函数放于如下位置：

1
2
3
4
5
public static void main(String[] args) {
    LKAES lkaes = new LKAES();
    lkaes.traceAESRead();
    lkaes.call_wbaes();
}

运行结果如图：

将这几千条记录拷贝出来，保存在trace.txt 中，在Python中做可视化，这十分方便。需要安装matplotlib以及numpy库。

1
2
3
4
5
6
7
import matplotlib.pyplot as plt
import numpy
 
input = numpy.loadtxt("trace.txt", int)
 
plt.plot(range(len(input)), input)
plt.show()

运行后生成折线图，将其放大是如下效果

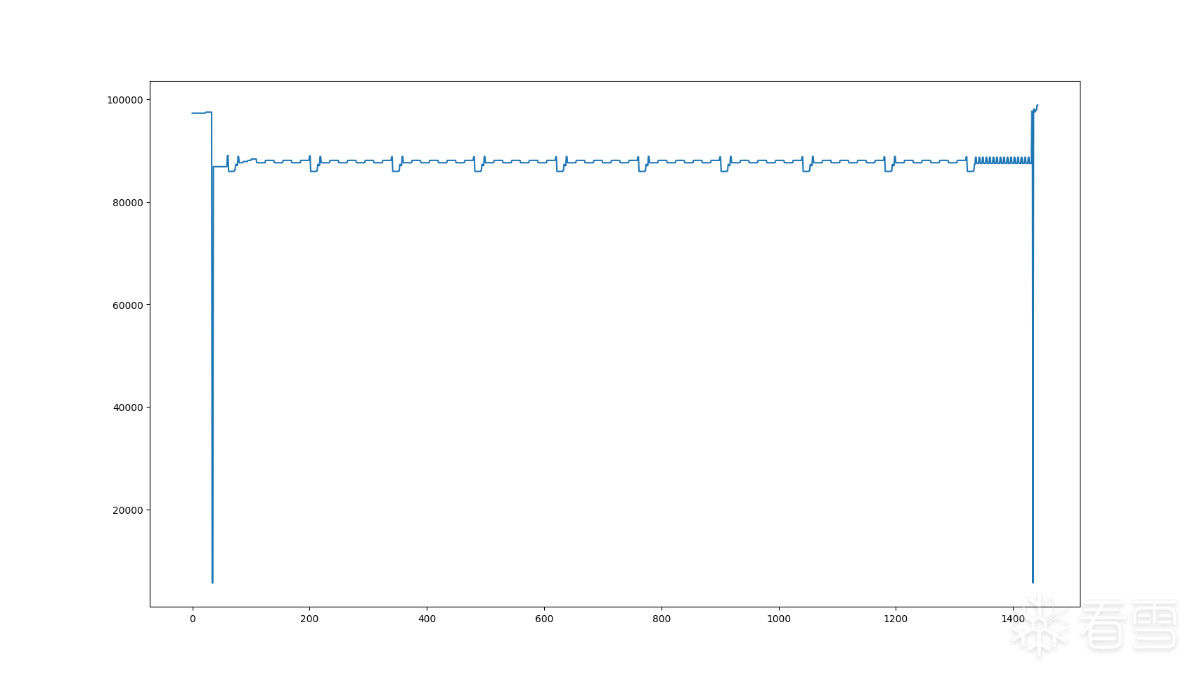
X轴的计数单位是次数，表示当前是第几次内存访问，如图，在程序的运行过程中，发生了1400余次对SO内存的读操作。Y轴是发起访问的偏移地址。需要注意，X与Y轴的数值表示为十进制。图上可得，Y主要在80000-100000之间，我们修改Y轴范围，增强呈现效果。

1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
import numpy
 
input = numpy.loadtxt("trace.txt", int)
 
# 限制Y
plt.ylim(80000,100000)
plt.plot(range(len(input)), input)
plt.show()

运行后

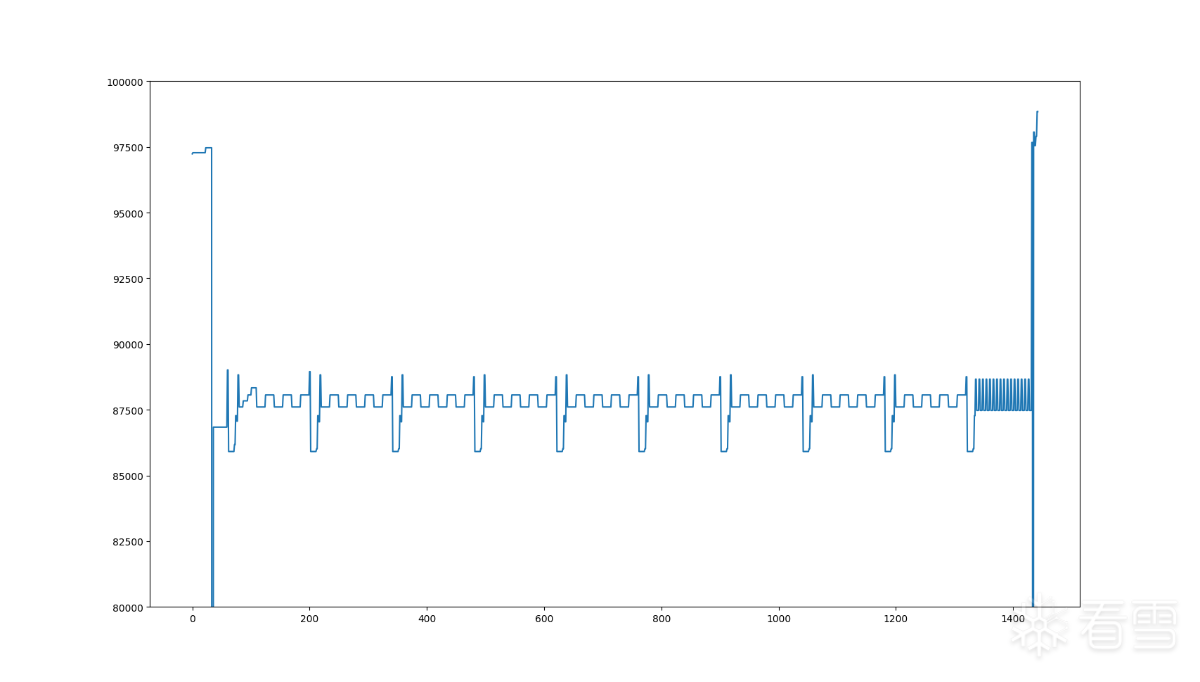
似乎还可以缩小到85000-90000之间，再次缩小Y的范围

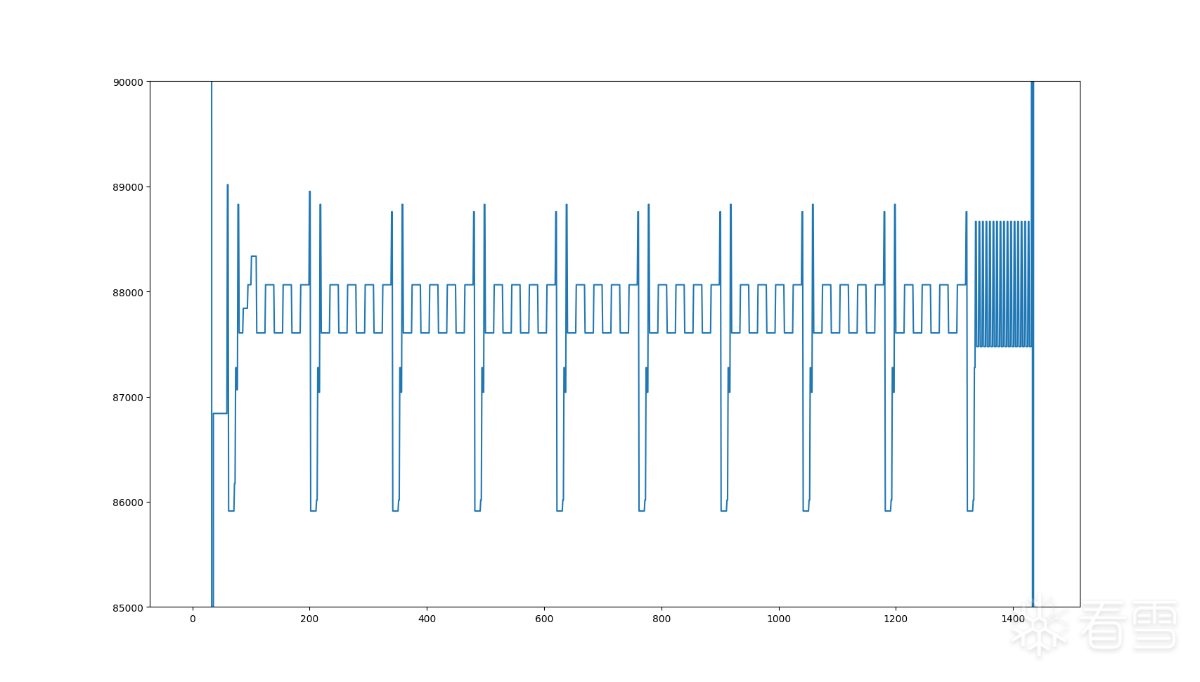
这样看着顺眼多了，我们对它进行分析。

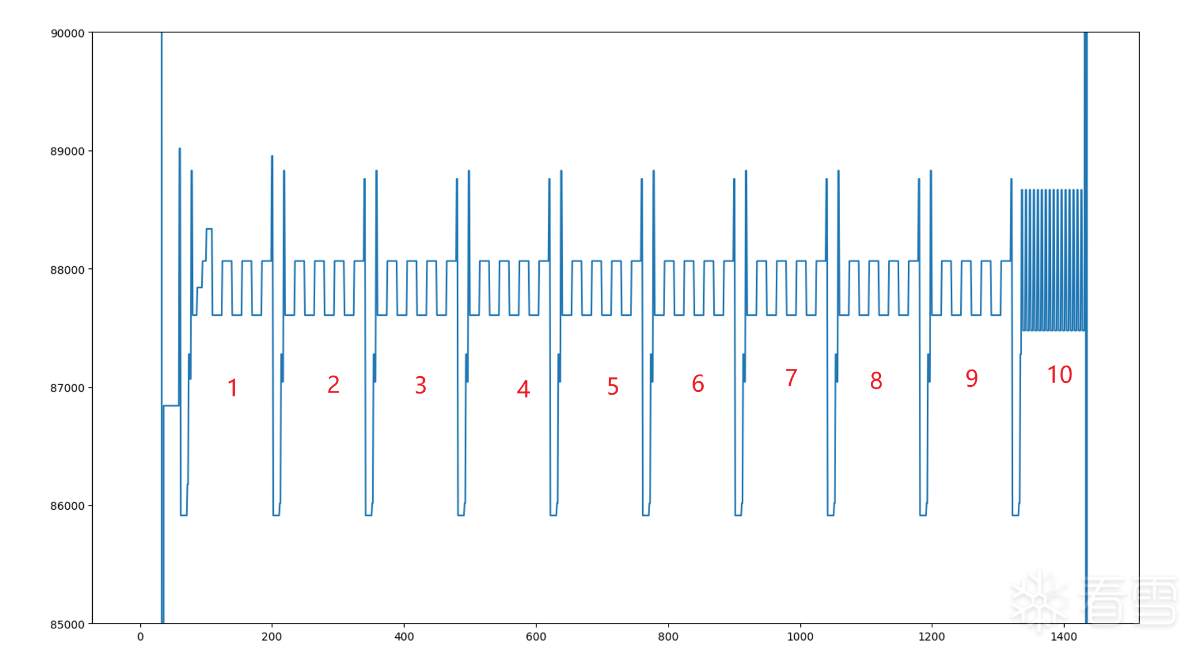
首先，可以比较明显的看到，存在十个重复的模式，这代表了十轮运算。这一点是有用的，可用于区分AES-128/192/256，分别对应10/12/14 轮。

除此之外，我们发现每轮运算的起点是一个较低的地址，具体在86000附近左右，转成十六进制就是0x14FF0附近。

在IDA 中查看该处，我们发现正是上一篇中所分析的wbShiftRows中。这就是我说的”Unidbg中的另一个好办法“，这得益于Unidbg中获取执行流非常容易。

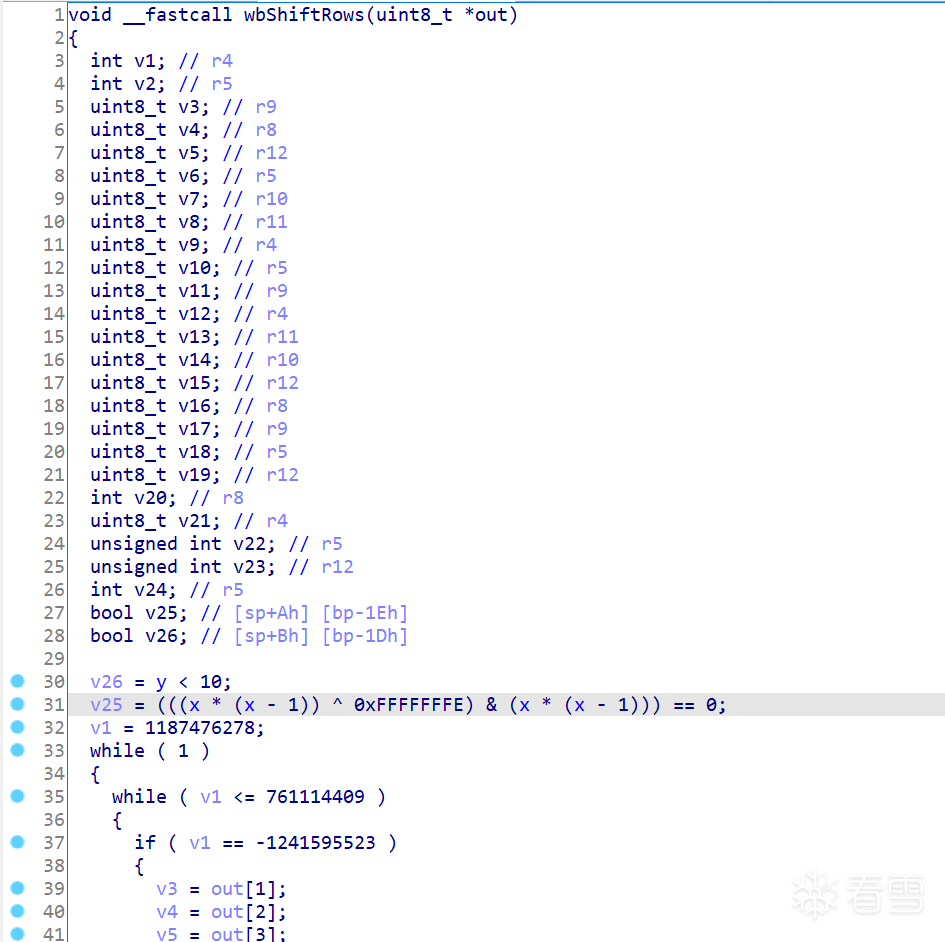
接下来就再次来到故障攻击的部分，整个代码近似于Frida Hook代码的复刻。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
package com.luckin;
 
import com.github.unidbg.AndroidEmulator;
import com.github.unidbg.Emulator;
import com.github.unidbg.Module;
import com.github.unidbg.arm.backend.Backend;
import com.github.unidbg.arm.backend.ReadHook;
import com.github.unidbg.arm.backend.UnHook;
import com.github.unidbg.arm.context.RegisterContext;
import com.github.unidbg.debugger.BreakPointCallback;
import com.github.unidbg.linux.android.AndroidEmulatorBuilder;
import com.github.unidbg.linux.android.AndroidResolver;
import com.github.unidbg.linux.android.dvm.AbstractJni;
import com.github.unidbg.linux.android.dvm.DalvikModule;
import com.github.unidbg.linux.android.dvm.VM;
import com.github.unidbg.memory.Memory;
import com.github.unidbg.memory.MemoryBlock;
import com.github.unidbg.pointer.UnidbgPointer;
import unicorn.ArmConst;
 
import java.io.File;
import java.io.IOException;
import java.nio.charset.StandardCharsets;
import java.util.Random;
 
public class LKAES extends AbstractJni {
    private final AndroidEmulator emulator;
    private final VM vm;
    private final Module module;
 
    public LKAES(){
        emulator = AndroidEmulatorBuilder.for32Bit().build(); // 创建模拟器实例，要模拟32位或者64位，在这里区分
 
        // 模拟器的内存操作接口
        final Memory memory = emulator.getMemory();
        // 设置系统类库解析
        memory.setLibraryResolver(new AndroidResolver(23));
        // 创建Android虚拟机
        vm = emulator.createDalvikVM(new File("unidbg-android/src/test/resources/luckin/ruixingkafei_4.9.3.apk"));
        vm.setVerbose(true);
        // 加载so到虚拟内存
        DalvikModule dm = vm.loadLibrary("cryptoDD", true);
        module = dm.getModule();
        // 设置JNI
        vm.setJni(this);
        dm.callJNI_OnLoad(emulator);
    }
 
    public static byte[] hexStringToBytes(String hexString) {
        if (hexString.isEmpty()) {
            return null;
        }
        hexString = hexString.toLowerCase();
        final byte[] byteArray = new byte[hexString.length() >> 1];
        int index = 0;
        for (int i = 0; i < hexString.length(); i++) {
            if (index  > hexString.length() - 1) {
                return byteArray;
            }
            byte highDit = (byte) (Character.digit(hexString.charAt(index), 16) & 0xFF);
            byte lowDit = (byte) (Character.digit(hexString.charAt(index + 1), 16) & 0xFF);
            byteArray[i] = (byte) (highDit << 4 | lowDit);
            index += 2;
        }
        return byteArray;
    }
 
    public static String bytesTohexString(byte[] bytes) {
        StringBuffer sb = new StringBuffer();
        for(int i = 0; i < bytes.length; i++) {
            String hex = Integer.toHexString(bytes[i] & 0xFF);
            if(hex.length() < 2){
                sb.append(0);
            }
            sb.append(hex);
        }
        return sb.toString();
    }
 
    public void call_wbaes(){
        MemoryBlock inblock = emulator.getMemory().malloc(16, true);
        UnidbgPointer inPtr = inblock.getPointer();
        MemoryBlock outblock = emulator.getMemory().malloc(16, true);
        UnidbgPointer outPtr = outblock.getPointer();
        byte[] stub = hexStringToBytes("30313233343536373839616263646566");
        assert stub != null;
        inPtr.write(0, stub, 0, stub.length);
        module.callFunction(emulator, 0x17bd5, inPtr, 16, outPtr, 0);
        String ret = bytesTohexString(outPtr.getByteArray(0, 0x10));
        System.out.println(ret);
        inblock.free();
        outblock.free();
    }
 
    public static int randInt(int min, int max) {
        Random rand = new Random();
        return rand.nextInt((max - min) + 1) + min;
    }
 
    public void dfaAttack(){
        emulator.attach().addBreakPoint(module.base + 0x14F98 + 1, new BreakPointCallback() {
            int count = 0;
            UnidbgPointer pointer;
            @Override
            public boolean onHit(Emulator<?> emulator, long address) {
                count += 1;
                RegisterContext registerContext = emulator.getContext();
                pointer = registerContext.getPointerArg(0);
                emulator.attach().addBreakPoint(registerContext.getLRPointer().peer, new BreakPointCallback() {
                    @Override
                    public boolean onHit(Emulator<?> emulator, long address) {
                    if(count % 9 == 0){
                        pointer.setByte(randInt(0, 15), (byte) randInt(0, 0xff));
                    }
                    return true;
                    }
                });
 
                return true;
            }
        });
    }
 
    public void traceAESRead(){
        emulator.getBackend().hook_add_new(new ReadHook() {
            @Override
            public void hook(Backend backend, long address, int size, Object user) {
                long now = emulator.getBackend().reg_read(ArmConst.UC_ARM_REG_PC).intValue();
                if((now>module.base) & (now < (module.base+module.size))){
                    System.out.println(now - module.base);
                }
            }
 
            @Override
            public void onAttach(UnHook unHook) {
 
            }
 
            @Override
            public void detach() {
 
            }
        }, module.base, module.base+module.size, null);
    }
 
 
    public static void main(String[] args) {
        LKAES lkaes = new LKAES();
//        lkaes.traceAESRead();
        lkaes.dfaAttack();
        for(int i =0;i<200;i++){
            lkaes.call_wbaes();
        }
 
    }
}

将正确密文与运行出的故障密文放入phoenixAES以及stark，可以得到和前文相同的结果。

五、总结

在这篇文章中，我们主要处理了用什么工具实现故障，以及捕获故障密文，并分别用源码以及 Unidbg 的方式进行了DFA 攻击演练。但是也只学了很少关于白盒、关于分析白盒密钥的知识，当你真正需要逆向一个白盒加密时，无法处理的概率远大于能处理的概率，在白盒内部会进行多维度的防御。接下来我们将尝试讲解白盒 aes具体的实现思路，一步步看一下如何将逻辑操作转换成查表操作，以及如何应对 DFA 等攻击行为，本想两篇文章讲解结束，奈何篇幅过于长...



更多【密码应用-白盒AES算法详解(二)】相关视频教程：www.yxfzedu.com




相关文章推荐

记录自己的技术轨迹
文章规则：
1)：文章标题请尽量与文章内容相符
2)：严禁色情、血腥、暴力
3)：严禁发布任何形式的广告贴
4)：严禁发表关于中国的政治类话题
5)：严格遵守中国互联网法律法规
6)：有侵权,疑问可发邮件至service@yxfzedu.com
近期原创 更多
友情链接
内核结构 FAQ
免责声明
课程目录
Windows内核
游戏逆向(FPS)
技术交流QQ群
342478842 215039827 137189196
314055665 159620936
微信公众号
www.yxfzedu.com是一个分享游戏安全,游戏外挂与反外挂,游戏驱动保护的视频网站！
接各种驱动定制如：游戏读写驱动，软件内存保护，防止调试等功能定制。
出租读写驱动，调试驱动，无痕注入支持各种游戏。
邮箱：service@yxfzedu.com
QQ：851920120
特别说明：不接游戏数据分析，外挂编写，登陆协议等类似业务。